PS/BOJ
[C++] 백준 1389 : 케빈 베이컨의 6단계 법칙
소-은
2024. 3. 19. 23:03
728x90
1. 문제
https://www.acmicpc.net/problem/1389
1389번: 케빈 베이컨의 6단계 법칙
첫째 줄에 유저의 수 N (2 ≤ N ≤ 100)과 친구 관계의 수 M (1 ≤ M ≤ 5,000)이 주어진다. 둘째 줄부터 M개의 줄에는 친구 관계가 주어진다. 친구 관계는 A와 B로 이루어져 있으며, A와 B가 친구라는 뜻
www.acmicpc.net
2. 문제 접근
문제를 이해하다보니 BFS로 풀면 되겠다고 답이 나왔다. 그래서, BFS 코드를 구현했더니 틀렸다. 문제를 제대로 안봤으니까.
결론적으로 1부터 5까지 각 숫자에 도달할 때까지 거리를 구하면 80%는 해결이다.
예시의 그래프는 아래와 같이 표현할 수 있다.
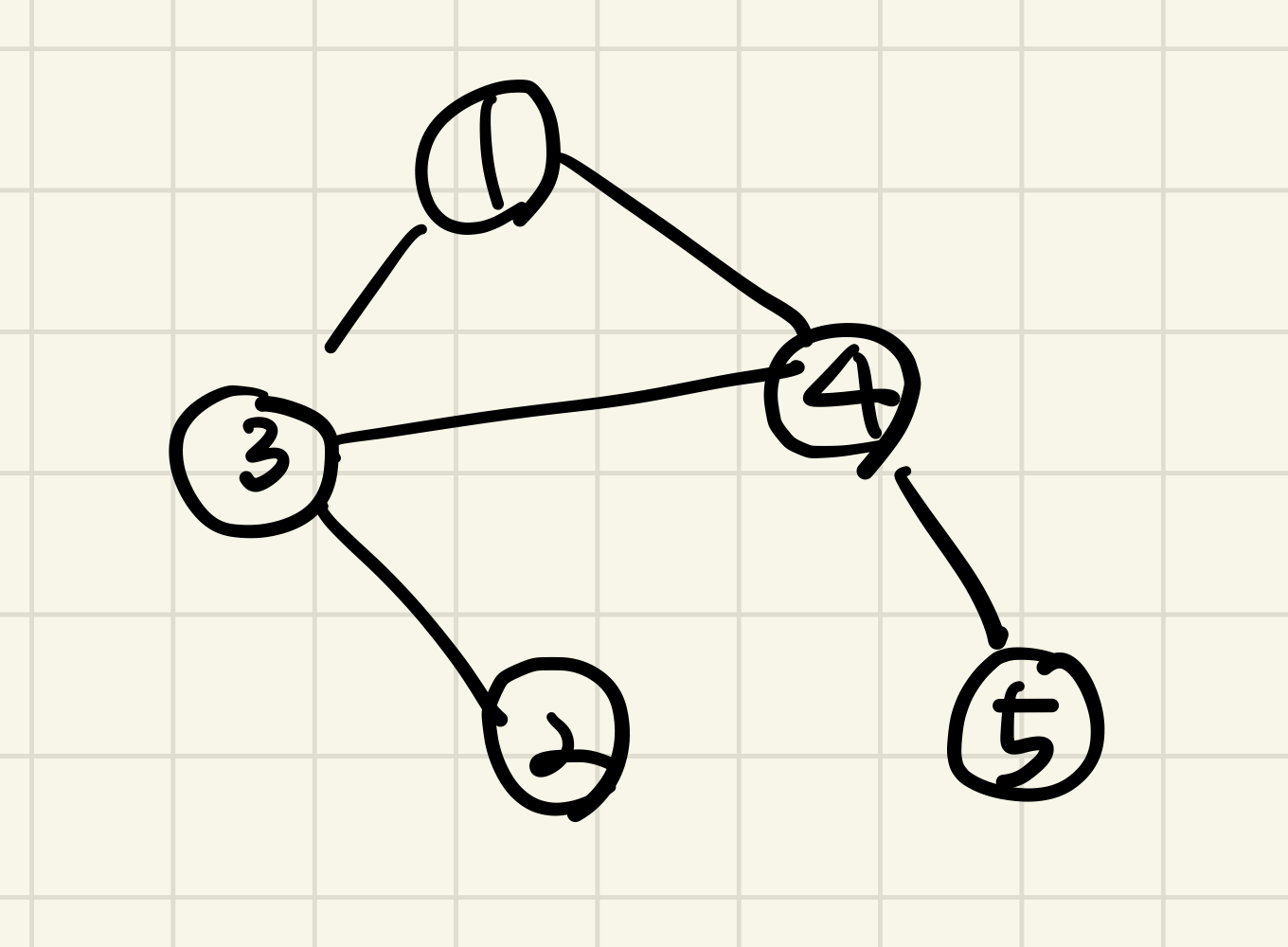
1부터 예시를 들면, 1은 2까지 [1-3-2]로 2단계, 3까지 1단계, 4까지 1단계, 5까지 [1-4-5]로 2단계, 따라서 총 2+1+1+2이다.
이를 생각해보면, BFS를 돌면서 B와 연결된 케빈 베이컨 수를 B의 케빈 베이컨 수에 1을 더한 값으로 저장하면 된다.
ans[j] = ans[i] + 1
이후 ans에 저장된 모든 원소의 합을 sum 배열에 하나씩 저장했고, 이 sum 배열에서 sum[i]가 가장 작은 값의 i 를 출력하면 된다.
3. 코드
#include <iostream>
#include <vector>
#include <queue>
#include <numeric>
using namespace std;
int n, m;
void bfs(vector<vector<int>> graph, int a);
vector<int> ans(101, 0);
int sum[101] = {0,};
int main() {
cin >> n >> m;
vector<vector<int>> graph(101, vector<int>(101, 0));
for (int i=0;i<m;i++) {
int a, b; cin >> a >> b;
graph[a][b] = 1; graph[b][a] = 1;
}
for (int i = 1; i<=n;i++) {
bfs(graph, i);
sum[i] = accumulate(ans.begin(), ans.end(), 0);
fill(ans.begin(), ans.end(), 0);
}
int min = sum[1]; int j = 1;
for (int i =1 ;i<=n;i++) {
if (sum[i] < min) {
min = sum[i];
j = i;
}
}
cout << j << "\n";
}
void bfs(vector<vector<int>> graph, int a) {
queue<int> q;
int visited[101] = {0,};
q.push(a);
visited[a] = 1;
while(!q.empty()) {
int i = q.front();
q.pop();
for (int j =1; j<=n;j++) {
if (!visited[j] && graph[i][j] == 1) {
q.push(j);
visited[j] = 1;
ans[j] = ans[i] + 1;
}
}
}
}728x90