이항계수

이항계수는 주어진 집합에서 원하는 개수만큼 순서에 상관없이 뽑는 조합의 개수를 의미한다. 이항계수는 위와 같은 수식으로 표현해 풀 수 있다. 알고리즘적으로 조금 더 쉽게 풀어보면 아래 수식과 같다.

이항계수를 계산하는 방법은 2가지가 있다. Divide-and-Conquer과 Dynamic Programming으로 푸는 방법이다.
Divide-and-Conquer
k 가 0이거나 n이 k일 때는 1을 리턴하고, 그게 아니라면 재귀를 반복한다. 아래와 같이 코드를 짤 수 있다.
typedef unsigned long long LongInteger;
LongInteger bin(int n, int k) {
if (k == 0 || n == k)
return 1;
else
return bin(n - 1, k) + bin(n - 1, k - 1);
}
그러나, 이 방법은 비효율적이다. 시간복잡도를 계산해보면 exponential하고 같은 값을 여러 번 계산하는 overlapping subproblem이 발생한다.
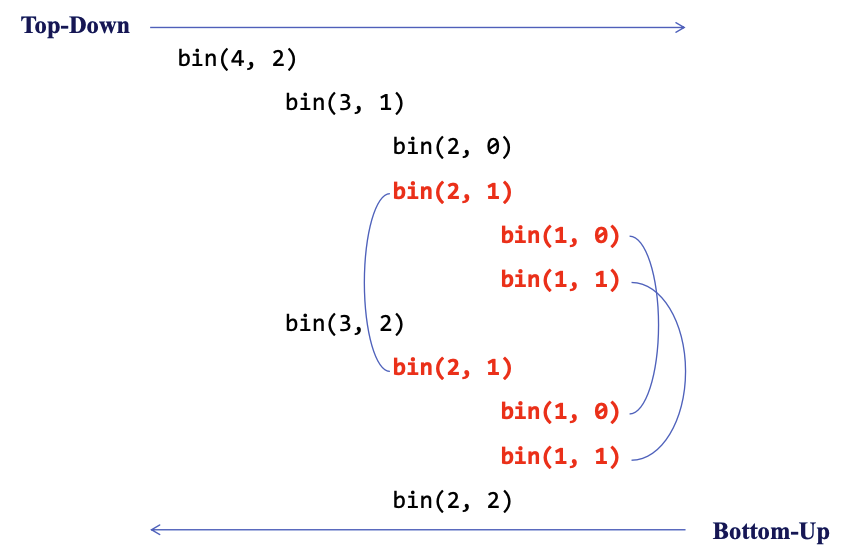
위 그림처럼 bin(3,1)과 bin(3,2)를 계산하는데 bin(2,1)을 중복으로 계산해야 한다.
이때 시간 복잡도를 계산하면 O(nCk)이다. 중복이 많고 시간복잡도가 크기 때문에 다른 방법을 사용해야 한다.
따라서, 중복을 제외하고 풀 수 있는 Bottom-up 방법인 Dynamic Programming을 사용할 것이다.
Dynamic Programming

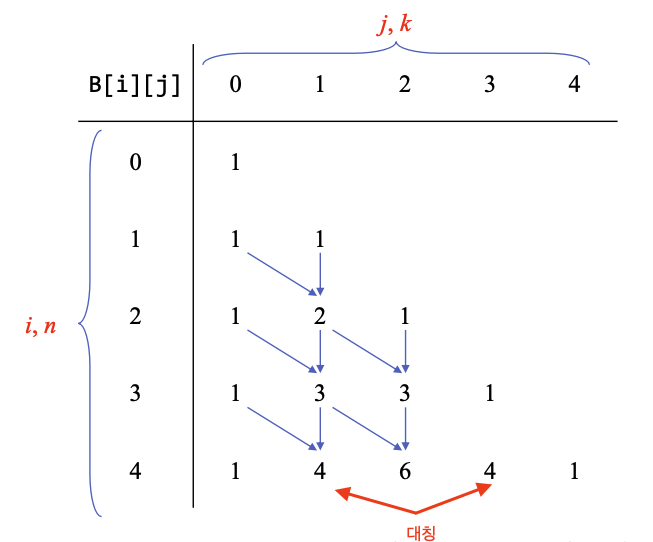
재귀관계식은 구했으니, 최적값을 저장하는 배열을 만들어보자. B[i][j]는 i, j를 저장하는 배열로, 관계식을 만들면 위 그림과 같다. 배열로 계산하면 아래 그림과 같은데, 이는 파스칼의 삼각형과 같다.
typedef unsigned long long LongInteger;
LongInteger bin2(int n, int k) {
vector<vector<LongInteger>> B(n + 1, vector<LongInteger>(n + 1));
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= min(i, k); j++) { // 이후로는 할 필요가 없다.
if (j == 0 || j == i)
B[i][j] = 1;
else
B[i][j] = B[i - 1][j] + B[i - 1][j - 1];
}
}
return B[n][k];
}
시간복잡도를 계산해보자.
i = 0일 때 1번, i = 1일 때 2번, i = 3일 때 3번, k일 때는 k+1번이다. 결국 B 배열을 순회하는 것이기 때문에 O(nk)이다.
Divide-and-Conquer보다는 훨씬 개선된 알고리즘이라 할 수 있다.
Dynamic Programming보다 더 효율적인 알고리즘은 무엇일까?
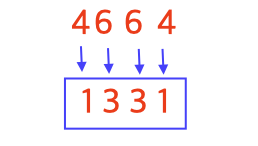
2차원 배열을 사용하는 대신에, 1차원 배열을 사용해서 아래 그림과 같이 덮어쓰기하면 가능하다.
LongInteger bin2(int n, int k) {
vector<LongInteger> B(k+1, 0);
B[0]=1;
for (int i = 1; i <= n; i++) {
for (int j = min(i, k); j>0;--j)
{
B[j] = (B[j]+B[j-1])%10007;
}
}
return B[k];
}
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최적 이진 탐색 트리(Optimal Binary Search Trees) (0) | 2024.04.10 |
|---|---|
| [알고리즘] 연쇄 행렬 곱셈(Chained Matrix Multiplication) (0) | 2024.04.10 |
| [알고리즘] 플로이드 알고리즘(Floyd Algorithm) (1) | 2024.04.10 |
| [알고리즘] 연속 부분 수열의 합 (0) | 2022.06.20 |
| [알고리즘] Sliding Window(슬라이딩 윈도우) Algorithm (0) | 2022.06.19 |
