Optimal Binary Search Trees
이진 탐색 트리에서 평균 탐색 비용을 최적화하는 알고리즘이다. 이진 탐색 트리에 대한 내용은 [자료구조] Tree(트리) - 이진 트리를 참고하면 된다. 간단하게 이진 탐색 트리의 성질은 다음과 같다.
- 각 노드는 하나의 유일한 key를 가진다.
- 모든 노드의 key는 그 노드의 왼쪽 서브 트리의 key보다 항상 크다.
- 모든 노드의 key는 그 노드의 오른쪽 서브 트리의 key보다 항상 작다.
문제 접근
n개의 key들이 배열 K에 정렬되어 있고, 각 key의 탐색 확률인 pi가 주어진다. 각 key의 비교 횟수는 ci이다.
이러한 조건에서 각 key의 평균 탐색 비용는 pi * ci이다.
먼저, Brute Force로 접근해보자. 모든 경우에 대해 최적의 이진 트리를 선택할 것이다.
n = 3, K = [10, 20, 30], p = [0.7, 0.2, 0.1]일 때, 이진 트리의 갯수는 총 5가지이다. 평균 탐색 비용 pi * ci를 각각 구하면, 1.4일 때 최적의 이진트리를 가진다고 할 수 있다.
이를 이용해 재귀 관계식을 만들어 보면, 먼저 배열 A를 이진 탐색 트리를 만드는데 최적의 탐색 비용을 저장한다.
우리의 목표는 Ki, ..., Kj를 (Ki, ..., Kk-1)Kk(Kk+1, ..., Kj)로 분할하는 재귀 관계식을 만드는 것이다.
Bottom-up 방법으로 재귀 식을 구하면, 아래 그림과 같다.
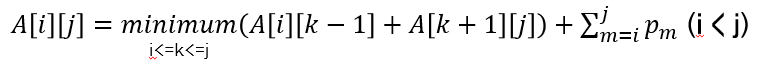
이때, 최적의 BST 모양을 알기 위해서, 배열 A에 최적의 탐색 비용을 저장하면서 배열 R에 해당 칸의 최적의 탐색 비용이 나오는 노드 번호를 저장한다. 즉, i번째 key부터 j번째 key까지를 이용해서 BST를 만들 때, 루트가 되는 노드 번호를 의미한다. R[1][n]을 구하면, 최적의 BST 루트 노드를 구할 수 있다.
int minimum(int i, int j, int& mink, vector<int>& d, matrix_t& M) {
int minValue = INF, value, sum;
for (int k = i; k <= j; k++) {
sum = 0;
for (int m = i; m<=j; m++) sum += d[m];
value = M[i][k-1] + M[k + 1][j] + sum;
if (minValue > value) {
minValue = value;
mink = k;
}
}
return minValue;
}
void optsearchtree(int n, vector<int>& p, matrix_t& A, matrix_t& R) {
for (int i = 1; i <= n; i++) {
A[i][i - 1] = 0; A[i][i] = p[i];
R[i][i - 1] = 0; R[i][i] = i;
}
A[n + 1][n] = R[n + 1][n] = 0;
for (int diagonal = 1; diagonal <= n - 1; diagonal++)
for (int i = 1; i <= n - diagonal; i++) {
int j = i + diagonal;
A[i][j] = minimum(i, j, k, p, A);
R[i][j] = k;
}
}'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] Knapsack Problem - Branch and Bound (0) | 2024.06.14 |
|---|---|
| [알고리즘] Knapsack Problem - Backtracking (0) | 2024.06.14 |
| [알고리즘] 연쇄 행렬 곱셈(Chained Matrix Multiplication) (0) | 2024.04.10 |
| [알고리즘] 플로이드 알고리즘(Floyd Algorithm) (1) | 2024.04.10 |
| [알고리즘] 이항계수(The Binomial Coefficient) (0) | 2024.04.10 |
