이전 글에서는 Knapsack problem을 Backtracking으로 접근하여 최적 해를 구했다. 이 방법은 bound가 maxprofit보다 크지 않을 때 non-promising이라고 판단한다. 알고리즘의 효율성을 따지면, 조금 더 나은 방법이 있다.
그 방법은 branch and bound로 접근하는 것이다. 이 방법의 특징을 잘 살리면 bound를 보고 판단하는 것 외에, promising한 노드들의 bound를 비교해서 그 중에서 가장 좋은 자식 노드들만 방문할 수 있다. DFS처럼 이미 정해진 순서대로 노드를 방문하는 것보다 더 빠르게 최적값을 찾을 수 있다. 이런 방법을 Best-First Search with branch and bound라고 한다. 이러한 방법은 BFS 방식을 약간 수정해서 접근할 수 있다. DFS(Backtracking)으로 푸는 방법에 비해서 BFS가 더 효율적인 것은 아니지만, Best-First Search 방법을 이해하기 위해서 BFS 방식을 소개할 것이다.
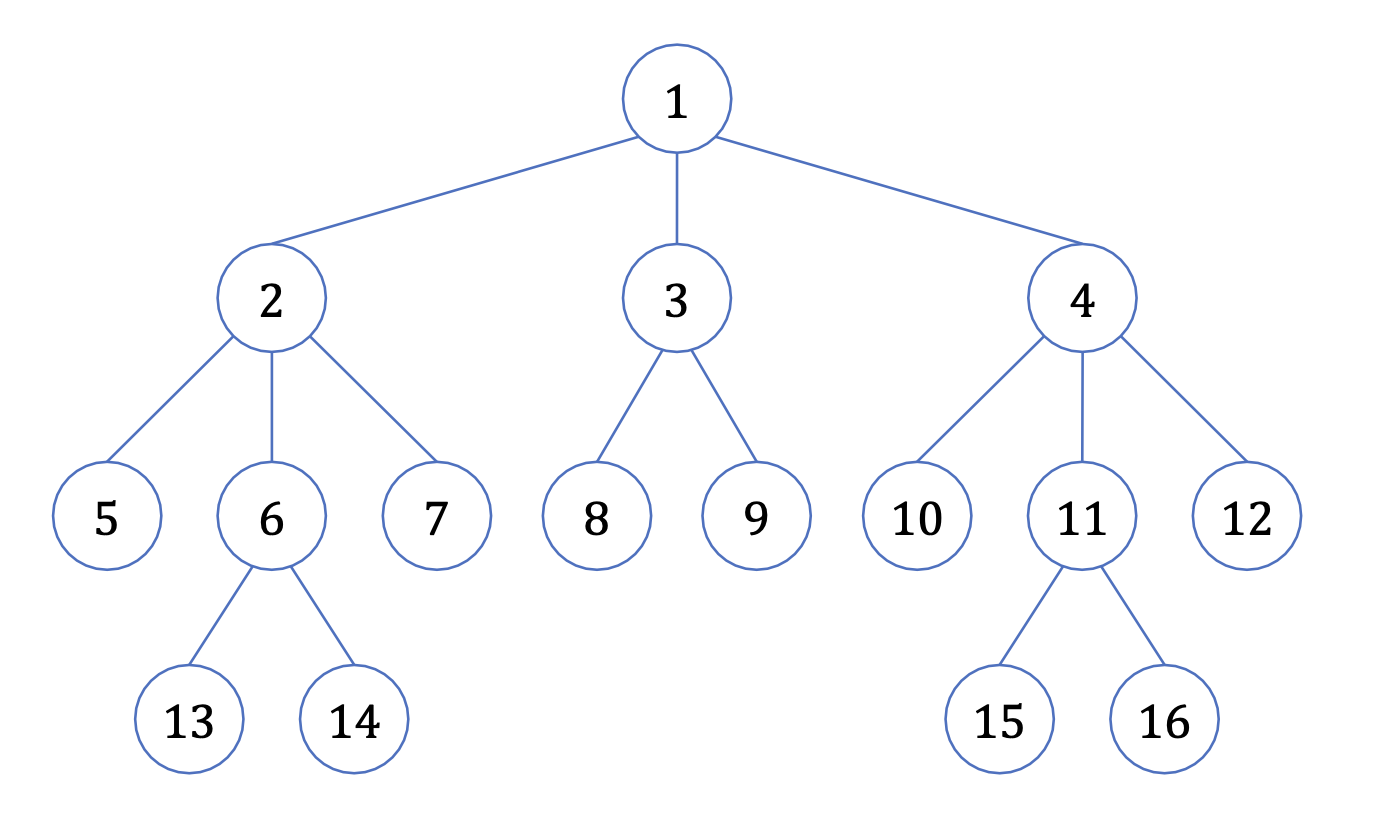
트리를 방문할 때 위와 같은 순서로 방문하게 된다. 이러한 방법을 0-1 knapsack problem에 적용해보자.
n = 4, W = 16일 때, 조건은 아래와 같다.
| i | 1 | 2 | 3 | 4 |
| pi | $40 | $30 | $50 | $10 |
| wi | 2 | 5 | 10 | 5 |
| pi/wi | $20 | $6 | $5 | $2 |
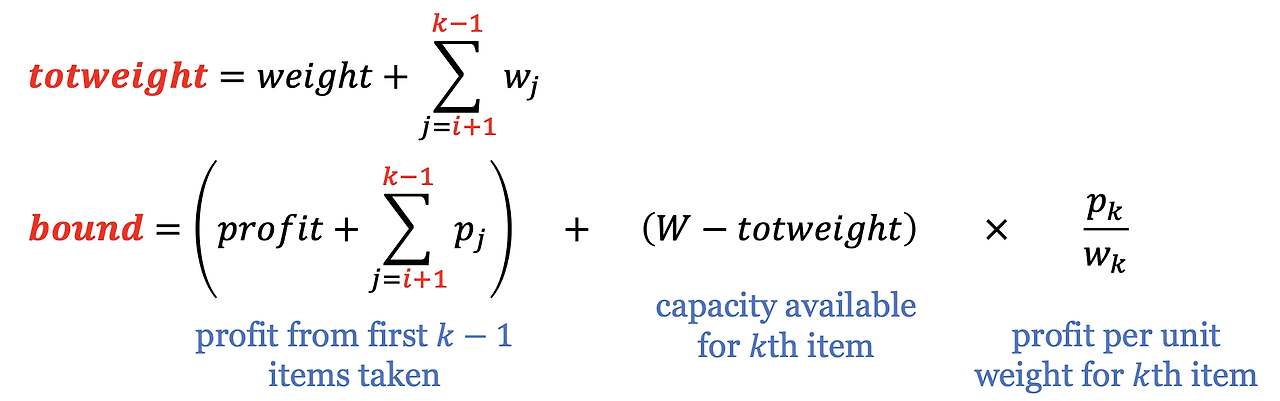
BFS로 knapsack 문제를 푸는 것은 DFS로 풀 때와 동일하다. 요약하자면, weight와 profit은 그 마디에 오기까지 포함된 아이템의 총 무게와 총 이익이다. 또 promising한지 판단하기 위해서 totweight, bound를 weight와 profit으로 초기화하고 totweight가 W를 초과하는 아이템에 도달할 때까지 Greedy하게 돌아간다. 이때 bound는 그 마디에서 얻을 수 있는 최대 이익을 말한다. maxprofit이 현재까지 찾은 최적 값일 때, bound가 maxprofit보다 작거나 같으면 non-promising으로 판단한다. 따라서 아래와 같은 식을 사용할 수 있다.
위의 과정을 통해서 상태공간트리를 만들어보면 아래와 같다.
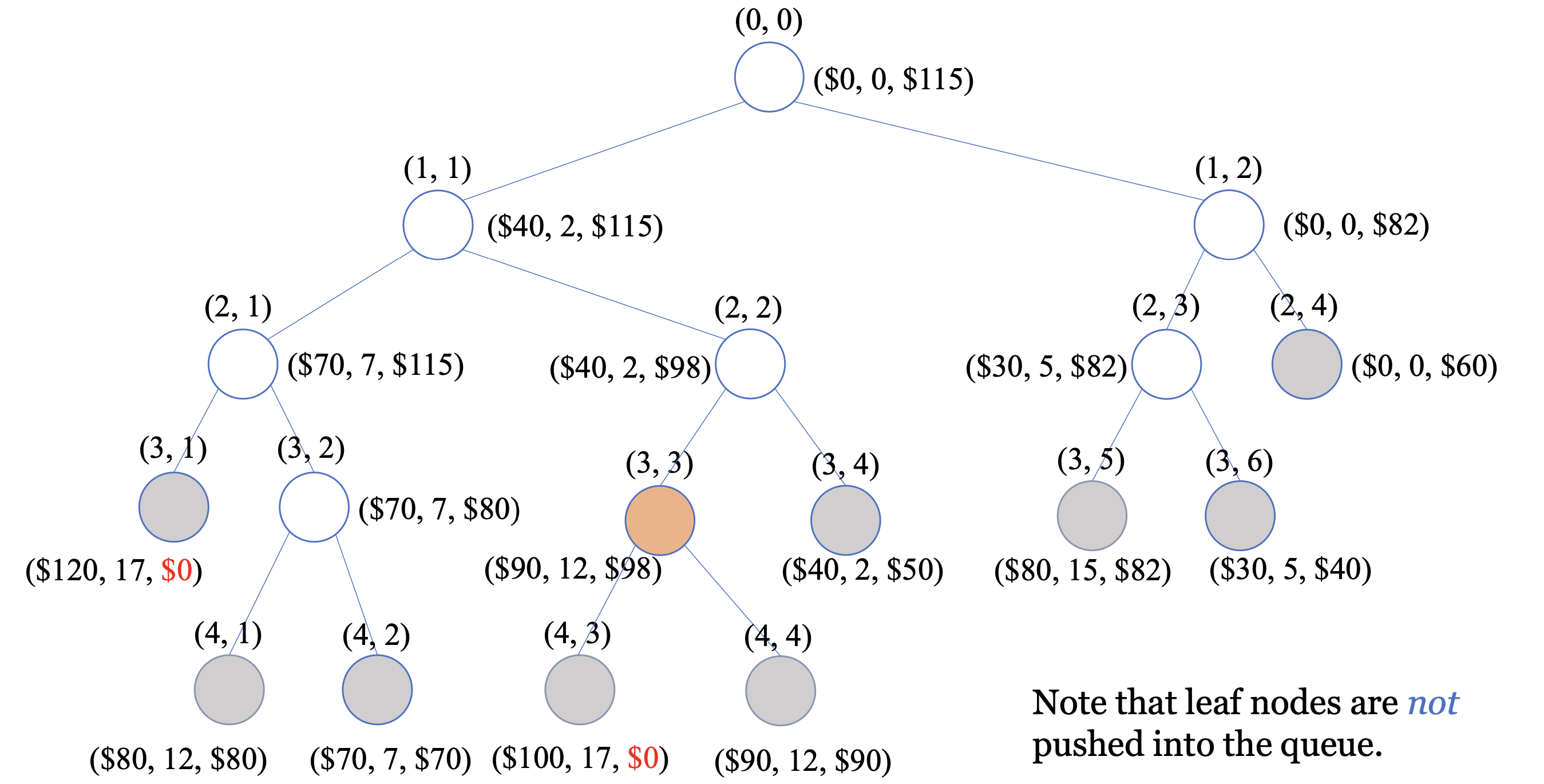
주목해야 할 것은 (3,1)과 (4,3) 노드이다. 이 노드들은 bound가 0으로 설정되어 있다. 이 알고리즘에서 promising인지 알기 위해서 지금까지의 최적값과 bound를 비교해서 더 좋은 것을 선택한다. 만약에 wi가 W보다 작지 않아서 non-promising하게 되면 bound를 0으로 설정해둔다. 이때 너비우선탐색의 경우에는 3번째 마디에서 maxprofit은 40이다. 그러나 이 시점에서 bound가 maxprofit을 넘기 때문에 그 마디 이후에도 확장할 수 있다. 어떤 마디의 자식 마디를 방문할지 말지는 그 마디를 방문할 때 결정하는데, 이때 maxprofit 값이 자식 마디를 방문하면서 바뀔 수 있다. 이렇게 되면 자식마디를 검사하는 시간을 낭비하게 되므로 Best-First Search에서는 이 낭비를 줄인다.
BFS 전략은 DFS 전략보다 효율적이라거나 딱히 좋은 점은 없다. 그러나 마디가 promising 한지 알기 위함이 아니라 다른 용도로 bound를 사용하면 낭비를 줄일 수 있다. 어떤 마디의 모든 자식마디를 방문해보고 promising하지만 방문하지 않은 마디들을 모두 살펴보고 난 후에, 그 중에서 bound 값이 좋은 마디를 우선적으로 확장하는 방법이다. 위와 같은 조건에서 상태공간트리를 만들어 보자.
그 전에, BFS 방법의 효율성을 높인 방법이 Best-First Search라고 했는데, 어떤 점이 바뀌었을까? BFS에서는 큐를 사용했는데, Best-First Search는 우선순위 큐를 사용한다. bound 값이 좋은 마디는 우선순위가 높아 먼저 처리된다.
처음 상태는 우선순위 큐에 (0,0)가 삽입된 상태이다.
먼저, (0,0)을 큐에서 제거하면서 root에 방문한다.
1. root 방문
- profit = 0, weight = 0
- totweight = 0+2+5 = 7
- bound = 0+40+30+(16-7)*5 = 115
- maxprofit = 0
2. (1,1) 방문
- profit = 0 + 40 = 40, weight = 0 + 2 = 2
- totweight = 2+5 = 7
- bound = 40+30+(16-7)*5 = 115
maxprofit보다 profit이 크므로 maxprofit = 40이다. (1,1)을 우선순위 큐에 삽입한다.
3. (1,2) 방문
- profit = 0, weight = 0
- totweight = 0 + 15
- bound = 0 + 80 + (16-15)*2 = 82
(1,2)를 우선순위 큐에 삽입한다.
4. 확장되지 않은 마디 중에서 가장 큰 bound을 가지면서 promising한 마디를 찾는다.
- (1,1) bound 115 > (1,2) bound 82
- (1,1)의 자식마디를 방문하므로 우선순위 큐에서 삭제한다.
5. (2,1) 방문
- profit = 70, weight = 7
- totweight = 7
- bound = 70+(16-7)*5 = 115
maxprofit보다 profit이 크므로 maxprofit = 70이다. (2,1)을 우선순위 큐에 삽입한다.
6. (2,2) 방문
- profit = 40, weight = 2
- totweight = 2+10=12
- bound = 40+50+(16-12)*2 = 98
(2,2)를 우선순위 큐에 삽입한다.
7. 확장되지 않은 마디 중에서 가장 큰 bound을 가지면서 promising한 마디를 찾는다.
- (2,1) bound 115 > (2,2) bound 98
- (2,1)의 자식마디를 방문하므로 우선순위 큐에서 (2,1)를 삭제한다.
8. (3,1) 방문
- profit = 120, weight = 17
weight > W이므로 나머지 값을 계산하지 않고 bound = 0으로 설정한다. 이때 우선순위 큐에 (3,1)을 삽입하면 안된다.
9. (3,2) 방문
- profit = 70, weight = 7
- totweight = 7+5=12
- bound = 70+10 = 80
(3,2)를 우선순위 큐에 삽입한다.
10. 확장되지 않은 마디 중에서 가장 큰 bound을 가지면서 promising한 마디를 찾는다.
- (2,2) bound 98 > (3,2) bound 80
- (2,2)의 자식노드를 방문하므로 우선순위 큐에서 삭제한다.
11. (3,3) 방문
- profit = 90, weight = 12
- totweight = 12
- bound = 90+(16-12)*2 = 98
maxprofit보다 profit이 크므로 maxprofit = 90이다.
(3,3)을 우선순위 큐에 삽입한다.
12. (3,4) 방문
- profit = 40, weight = 2
- totweight = 7
- bound = 10+40 = 50
maxprofit > bound 이므로 non-promising이다. 자식마디들을 방문하지 않는다.
따라서 우선순위 큐에 삽입하지 않는다.
13. 확장되지 않은 마디 중에서 가장 큰 bound을 가지면서 promising한 마디를 찾는다.
- (3,3) bound 98 > (1,2) bound 82
- (3,3)의 자식노드를 방문하므로 우선순위 큐에서 삭제한다.
14. (4,1) 방문
- profit = 100, weight = 17
weight > W이므로 나머지 값을 계산하지 않고 bound = 0으로 설정한다.
우선순위 큐에 (4,1)를 삽입하지 않는다.
15. (4,2) 방문
- profit = 90, weight = 12
- totweight = 12
- bound = 90
bound가 profit보다 작거나 크기 때문에 non-promising으로 판단한다. 따라서 우선순위 큐에 삽입하지 않는다.
promising 하면서 방문하지 않은 자식마디가 없으므로 끝낸다. 이와 같은 과정을 통해서 만들어진 트리는 아래와 같다.
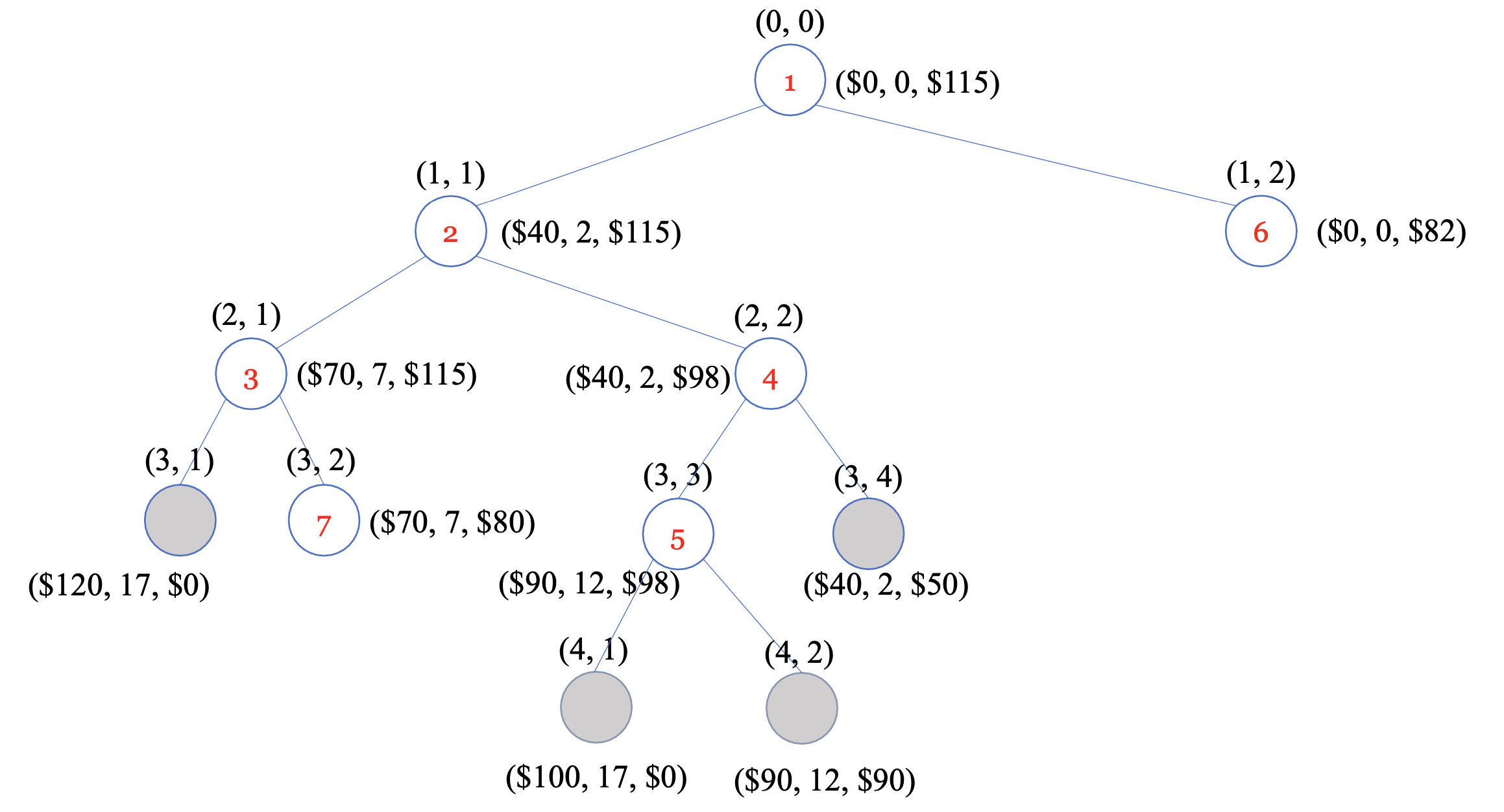
Depth-First, Breadth-First, Best-First 방식으로 만든 상태공간트리를 비교해보면, Depth-First는 총 13개의 노드, Breadth-First는 총 17개 노드, Best-First는 총 11개의 노드를 가진다. Backtracking 방식과 비교해서 2개 밖에 차이나진 않지만 큰 상태공간트리에서 Best-First 방식으로 최적해를 찾는 경우는 꽤나 큰 차이가 날 것이다.
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] The Selection Problem - Quick Sort (0) | 2024.06.17 |
|---|---|
| [알고리즘] The Selection Problem - 일반적인 경우 (0) | 2024.06.17 |
| [알고리즘] Knapsack Problem - Backtracking (0) | 2024.06.14 |
| [알고리즘] 최적 이진 탐색 트리(Optimal Binary Search Trees) (0) | 2024.04.10 |
| [알고리즘] 연쇄 행렬 곱셈(Chained Matrix Multiplication) (0) | 2024.04.10 |
