728x90
K번째로 작은 값 찾기
Quick sort
n과 K가 주어질 때 K 번째로 작은 값을 찾아야 한다. Quick Sort 방식으로 pivot보다 작은 것은 왼쪽, 큰 것은 오른쪽에 두고 pivot이 K번째에 위치할 때까지 재귀적으로 반복하여 푸는 방법이다.
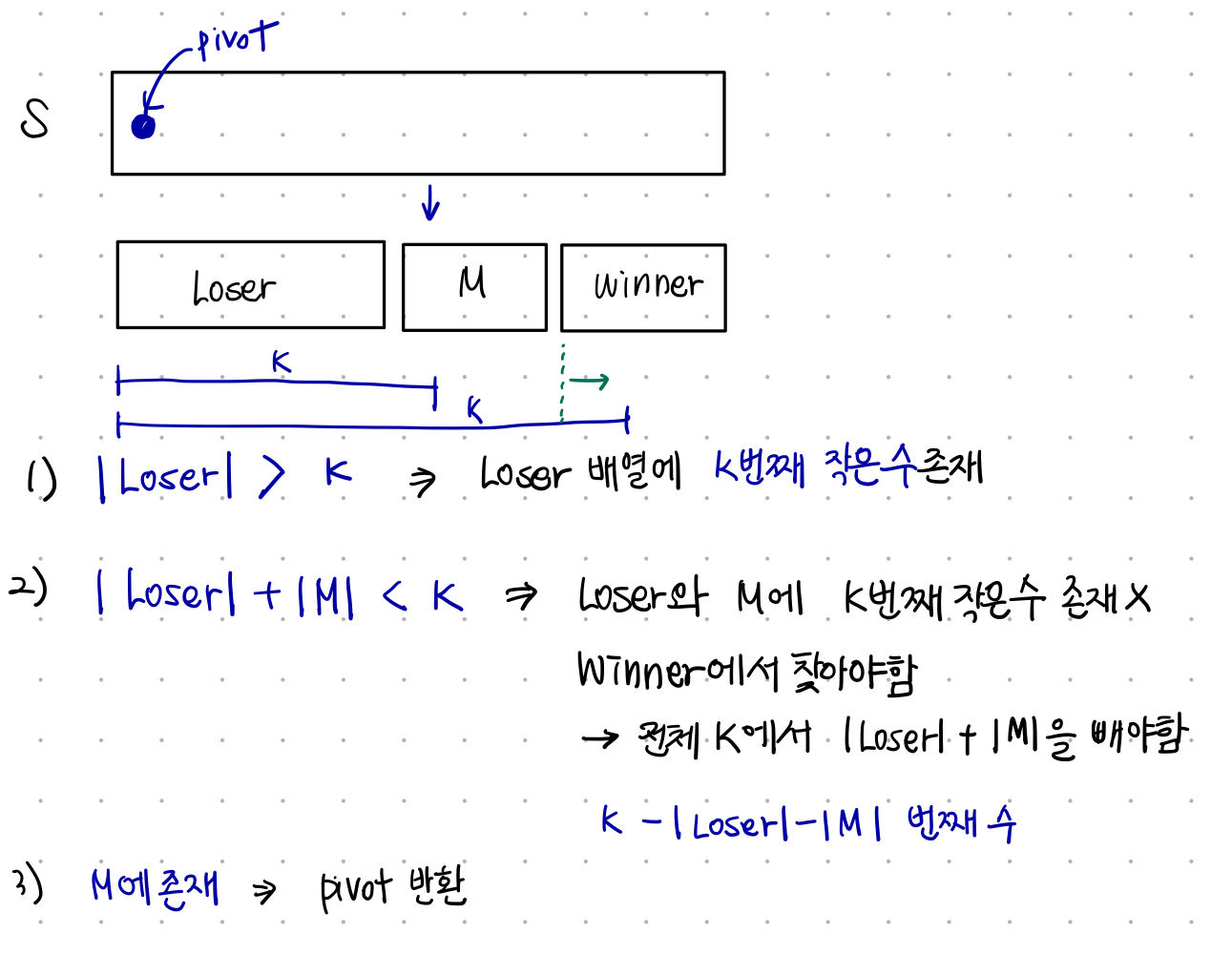
먼저 pivot을 선택한다음에 Loser 배열과 Winner 배열로 나눈다. Loser는 pivot보다 작고 Winner은 pivot보다 큰 값들의 배열이다. pivot과 같은 값이면 M 배열에 집어 넣는다. 이 배열들을 만들기 위해서는 n-1번의 비교가 필요하다.
- Loser 집합의 개수가 K보다 큰 경우
- 우리가 찾으려는 K가 Loser에 존재한다는 뜻으로, K번째 값을 반환하면 된다.
- Loser 집합의 개수와 M 집합의 개수가 K보다 작은 경우
- 우리가 찾으려는 K가 Loser, M에 존재하지 않는다는 뜻이다. 따라서 Winner에서 값을 찾아야 한다.
- Winner 배열에서 몇 번째에 존재하는지 알려면 전체 K에서 Loser와 M의 개수를 빼줘야 한다.
- M에 존재하는 경우
- M은 모두 pivot과 동일한 수만 존재하기 때문에 pivot을 반환하면 된다.
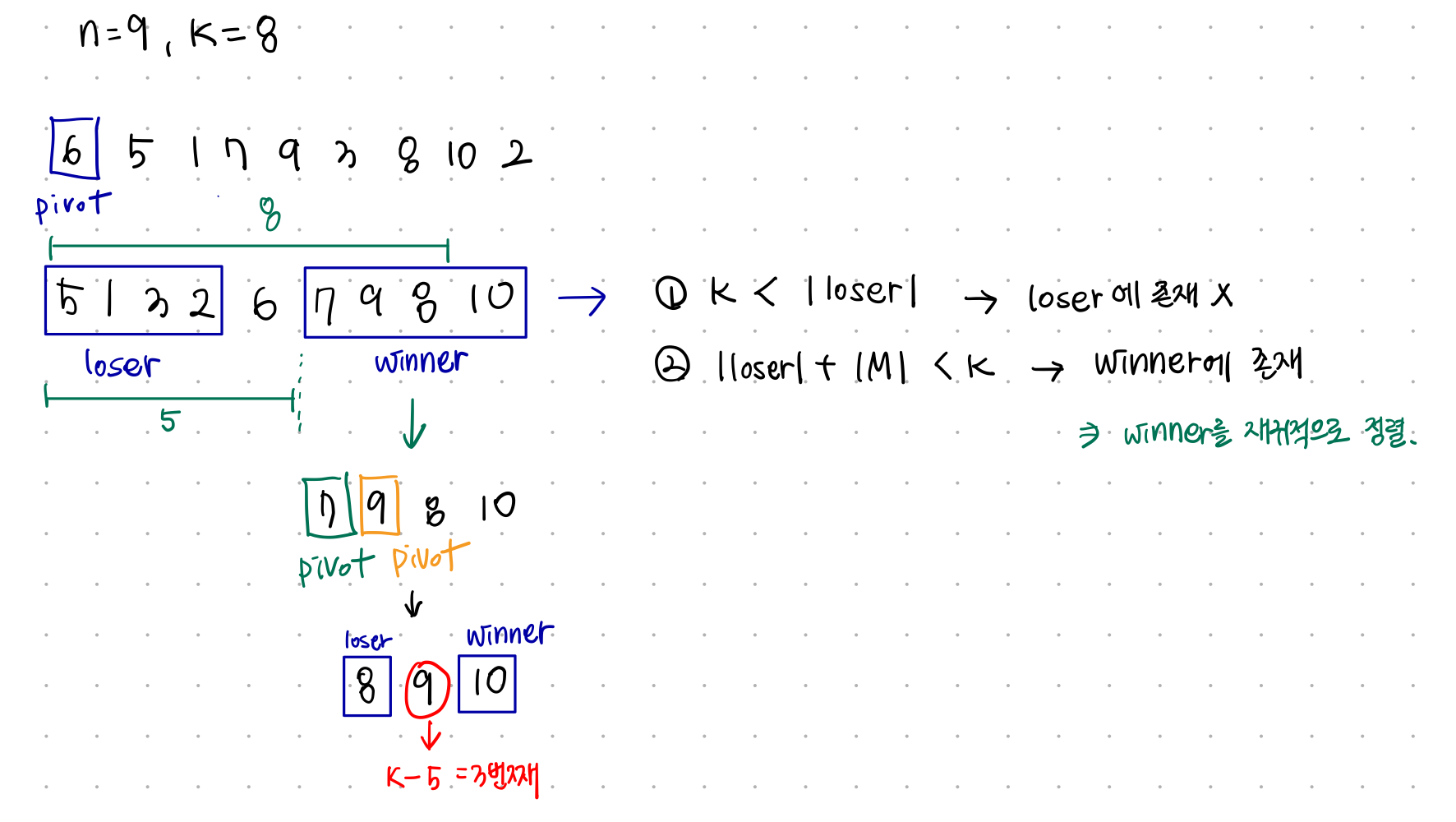
n = 9인 배열 S = [6, 5, 1, 7, 9, 3, 8, 10, 2]라고 하자. K = 8일 때, 8번째로 작은 수를 찾아야 한다. pivot = 6일 때, loser과 winner에 각각 pivot보다 작은수, 큰수를 넣는다. loser + M의 개수가 k보다 작기 때문에 winner 배열에서 K번째 값을 찾을 수 있다. K = 8이고 loser + M의 개수가 5이므로, winner 배열에서 (8-5)번째 값이 K번째로 작은 값이 된다.
값이 불균형으로 나뉘는 경우 최악의 경우로, T(n) = n(n-1)/2, O(n^2)의 시간복잡도를 가진다. 평균 시간복잡도는 pivot을 기준으로 n/2 개의 배열로 나뉜다면 T(n) = T(n/2) + n이고, O(n)의 시간복잡도를 가진다. 이러한 불균형을 줄이기 위해서 pivot을 잘 고르면 시간복잡도를 O(nlogn)만큼 줄일 수 있다.
728x90
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] Backtracking - Sum of Subsets (0) | 2024.06.18 |
|---|---|
| [알고리즘] The Selection Problem - Median of Medians (0) | 2024.06.17 |
| [알고리즘] The Selection Problem - 일반적인 경우 (0) | 2024.06.17 |
| [알고리즘] Knapsack Problem - Branch and Bound (0) | 2024.06.14 |
| [알고리즘] Knapsack Problem - Backtracking (0) | 2024.06.14 |
