Knapsack Problem은 아주 유명한 문제이다. 어떤 배낭이 있고 그 배낭에 넣을 수 있는 최대 무게가 W라고 하자. 배낭에 넣을 수 있는 n개의 물건이 각각 무게 wi와 이익 pi를 가지고 있을 때, 배낭이 최대한 비싼 물건들을 담을 수 있는 조합을 찾는 문제이다. knapsack 문제는 원하는 만큼 물건을 쪼개어 담는 문제인 Fractional Knapsack와 물건을 쪼갤 수 없어 무게와 가치가 무조건 정수형태를 가지는 0-1 Knapsack 두 유형으로 나뉜다. 이번에는 0-1 Knapsack 문제를 해결하는 방법에 대해서 생각해보자.
먼저 마디가 promising한지 판단해야 한다. Greedy Algorithm으로 접근하면, 해당 아이템의 무게가 배낭에 넣을 수 있는 최대 무게 W보다 크거나 같을 때를 non-promising으로 하였다. 또 이익 p가 높을 수록 좋으므로, 현재까지 p 중에서 가장 좋은 p를 선택했었다. 그러나 이 방법은 최적값을 구하기 어렵다.
그러면, promising한 지 판단하기 위한 근거를 더 설정해보자. 먼저 "가성비"를 고려하기 위해서 pi/wi 값을 내림차순으로 정렬한다. 그 마디에서 최대한으로 얻을 수 있는 이익이 얼마인지 고려하기 위해서 bound 변수를 설정한다. bound에는 pi 값이 계속해서 더해진다. 또한 totweight에는 W 값을 초과할 때까지 wi 값을 추가한다. 이때 W 값을 초과하는 마디의 레벨을 k라고 둔다.
정리하면, 아래와 같다.
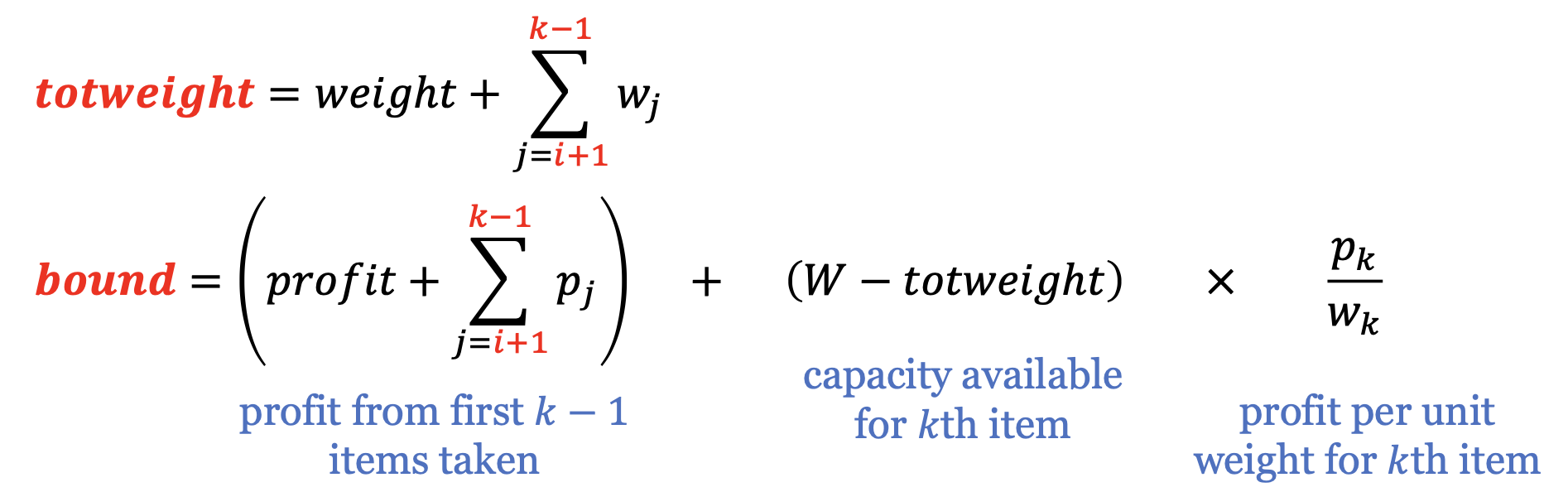
maxprofit이 현재까지의 최적 값이라고 할 때 bound가 maxprofit보다 커야지 promising하다고 판단한다. 이미 좋은 이익이 있는데 굳이 최대로 얻을 수 있는 값이 작은 마디를 탐색할 이유가 없다. 쉽게 말하면 같은 물건을 80% 할인하는 곳을 찾았는데 굳이 할인하지 않는 곳에 가서 물건을 찾는 건 의미가 없다. 그래서 bound가 maxprofit보다 작거나 같으면 non-promising이라고 판단하고 더이상 탐색하지 않는다.
예제를 통해서 상태공간트리를 만들어 보자.
| i | 1 | 2 | 3 | 4 |
| pi | $40 | $30 | $50 | $10 |
| wi | 2 | 5 | 10 | 5 |
| pi/wi | $20 | $6 | $5 | $2 |
처음에는 maxprofit = 0이다.
1. 루트 노드 방문
- profit = 0, weight = 0
- totweight = 0+2+5 = 7
- bound = 0+40+30+(16-7)*5 = 115
weight <= W이고 bound > maxprofit 이므로 promising하다. k는 W 값을 초과하는 w의 인덱스 값이다. 3번째까지 모두 더하면 17이므로 W를 넘는다.
2. (1,1) 방문
- profit = 0 + 40 = 40, weight = 0 + 2 = 2
- totweight = 2+5 = 7
- bound = 40+30+(16-7)*5 = 115
weight <= W이고 기존 maxprofit보다 profit이 더 좋기 때문에 maxprofit 값을 40으로 설정한다.
bound > maxprofit 이기 때문에 promising하다.
3. (2,1) 방문
- profit = 40 + 30 = 70, weight = 2 + 5 = 7
- totweight = 7
- bound = 70 + (16-7)*5 = 115
weight <= W이고 기존의 maxprofit 보다 profit이 더 좋기 때문에 maxprofit = 70이다.
또한 bound > maxprofit이므로 promising 노드이다.
4. (3,1) 방문
- profit = 70 + 50 = 120, weight = 7+10 = 17
weight > W이므로 non-promising이다. 나머지는 계산하지 않고 부모 노드로 돌아간다.
5. (3,2) 방문
- profit = 70, weight = 7
- totweight = 7
- bound = 70+10+(16-7)*0 = 80
weight <= W이고 bound > maxprofit 이므로 다음 노드를 방문한다.
이러한 과정을 계속해서 반복하면 아래와 같은 표와 상태공간트리가 완성된다.
| 노드 | p | w | totweight | bound | k | maxprofit | promising? |
| root (0,0) |
0 | 0 | 0+2+5=7 | 0+40+30+(16-7)*5 = 115 | 3 | 0 | (wi < W) && (bound > maxprofit) yes! |
| (1,1) | 40 | 2 | 2+5=7 | 40+30+(16-7)*5 = 115 | 3 | 0 -> 40 | (wi < W) && (bound > maxprofit) yes! |
| (2,1) | 70 | 7 | 7 | 70+(16-7)*5 = 115 | 3 | 40 -> 70 | (wi < W) && (bound > maxprofit) yes! |
| (3,1) | 120 | 12 | - | - | - | 70 | (wi >= W) no -> (2,1)로 backtracking |
| (3,2) | 70 | 7 | 7 | 70+10+(16-7)*0 = 80 | 5 | 70 | (wi < W) && (bound > maxprofit) yes! |
| (4,1) | 80 | 12 | 12 | 80+(16-7)*0 = 80 | 5 | 70 -> 80 | (bound <= maxprofit) no -> (3,2)로 backtracking |
| (4,2) | 70 | 7 | 7 | 70 | 5 | 80 | (bound <= maxprofit) no -> (1,1)로 backtracking |
| (2,2) | 40 | 2 | 2+10=12 | 40+50+(16-12)*2 = 98 | 4 | 80 | (wi < W) && (bound > maxprofit) yes! |
| (3,3) | 90 | 12 | 12 | 90+(16-12)*2 = 98 | 4 | 80 -> 90 | (wi < W) && (bound > maxprofit) yes! |
| (4,3) | 100 | 17 | - | - | - | 90 | (wi >= W) no -> (3,3)로 backtracking |
| (4,4) | 90 | 12 | 12 | 90+(16-12)*0 = 90 | 5 | 90 | (bound <= maxprofit) no -> (2,2)로 backtracking |
| (3,4) | 40 | 2 | 2+5=7 | 40+10+(16-7)*0 = 50 | 5 | 90 | (bound <= maxprofit) no -> root로 backtracking |
| (1,2) | 0 | 0 | 0 | 0+30+50+10+(16-0)*0 = 90 | 5 | 90 | (bound <= maxprofit) no -> root로 backtracking |
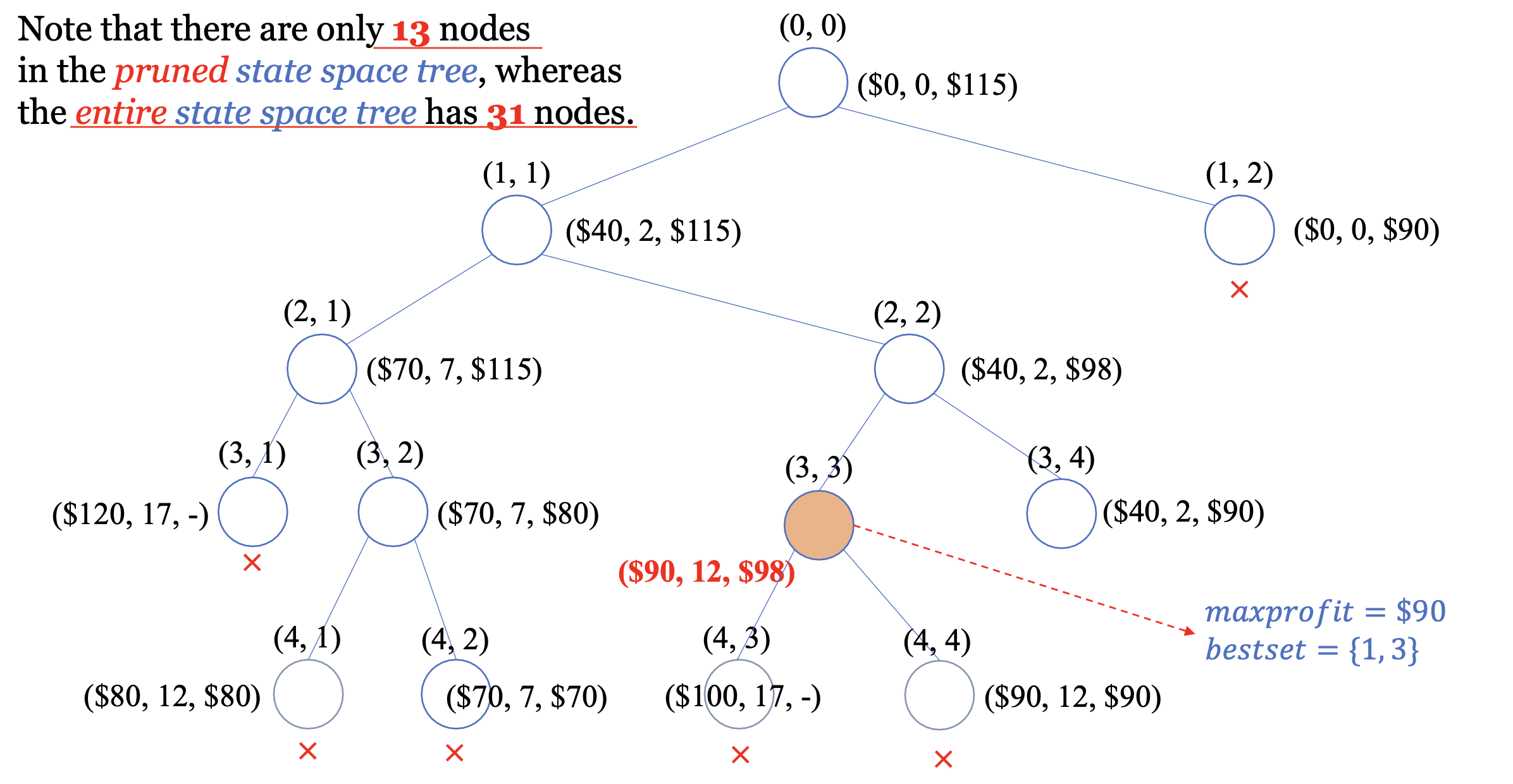
상태공간트리 방문 노드 수는 총 15개, original 상태공간트리의 노드는 총 31개이다.
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] The Selection Problem - 일반적인 경우 (0) | 2024.06.17 |
|---|---|
| [알고리즘] Knapsack Problem - Branch and Bound (0) | 2024.06.14 |
| [알고리즘] 최적 이진 탐색 트리(Optimal Binary Search Trees) (0) | 2024.04.10 |
| [알고리즘] 연쇄 행렬 곱셈(Chained Matrix Multiplication) (0) | 2024.04.10 |
| [알고리즘] 플로이드 알고리즘(Floyd Algorithm) (1) | 2024.04.10 |
