Chained Matrix Multiplication
연쇄 행렬 곱셈은 곱셈을 할 때 곱셈 연산을 최소로 하는 곱셈 순서를 찾는 알고리즘이다. 행렬에서 곱셈은 결합 법칙이 성립하기 때문에 곱셉 순서는 상관 없지만, 연산의 양이 달라진다.
예를 들어, 2 * 3 행렬 A와 3 * 5 행렬 B, 5 * 7 행렬 C가 있다고 하자. 이 행렬들의 곱 ABC를 구하는 경우는 2가지가 있다.
- (A * B) * C
- 연산 횟수 : 2 * 3 * 5 + 2 * 5 * 7 = 100
- A * (B * C)
- 연산 횟수 : 3 * 5 * 7 + 2 * 3 * 7 = 147
결과는 같지만 연산의 횟수가 달라진다는 것을 알 수 있다. 먼저 Brute Force로 접근해보자.
모든 경우의 수를 계산해야 하기 때문에 exponential 시간이 소요된다. 그렇다면, 작은 문제로 쪼개어 풀면 더 효율적이지 않을까? 예를 들어, (A1(A2(A3A4))) 이라면, A2(A3A4)를 먼저 계산하는 것이다.
문제 접근
이를 위해서 문제를 조금 더 간소화해보자.
n개의 연쇄 행렬 곱셈 A1 * ... * An이 있다. 행렬의 특성으로 인해, Ak-1의 행의 개수와 Ak의 열의 개수가 같아야 계산할 수 있다. 이때, dk를 행렬 Ak의 행의 개수로 정의하면, Ak+1의 열의 개수도 dk이다.
배열 M을 연쇄 행렬을 곱하는데 필요한 연산의 최소 횟수를 저장한다고 하자. 그렇다면 M[i][j]는 Ai부터 Aj까지 행렬을 곱하는데 필요한 연산의 최소 횟수라 할 수 있다. 우리의 목표는 Ai, ..., Aj 행렬을 (Ai, ... , Ak)(Ak+1, ..., Aj)로 작게 분할하는 것이다. 따라서 재귀 관계식은 아래 그림과 같다.
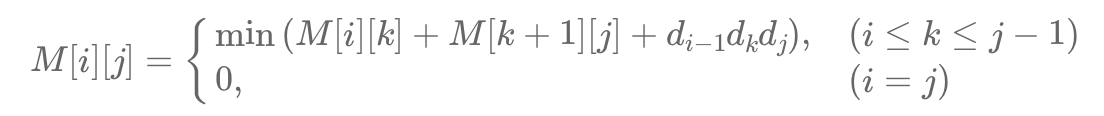
간단하게 말하면, M[i][j]은 각 부분 행렬의 곱셈 횟수와 두 행렬의 곱셈 횟수를 더한 값이다.
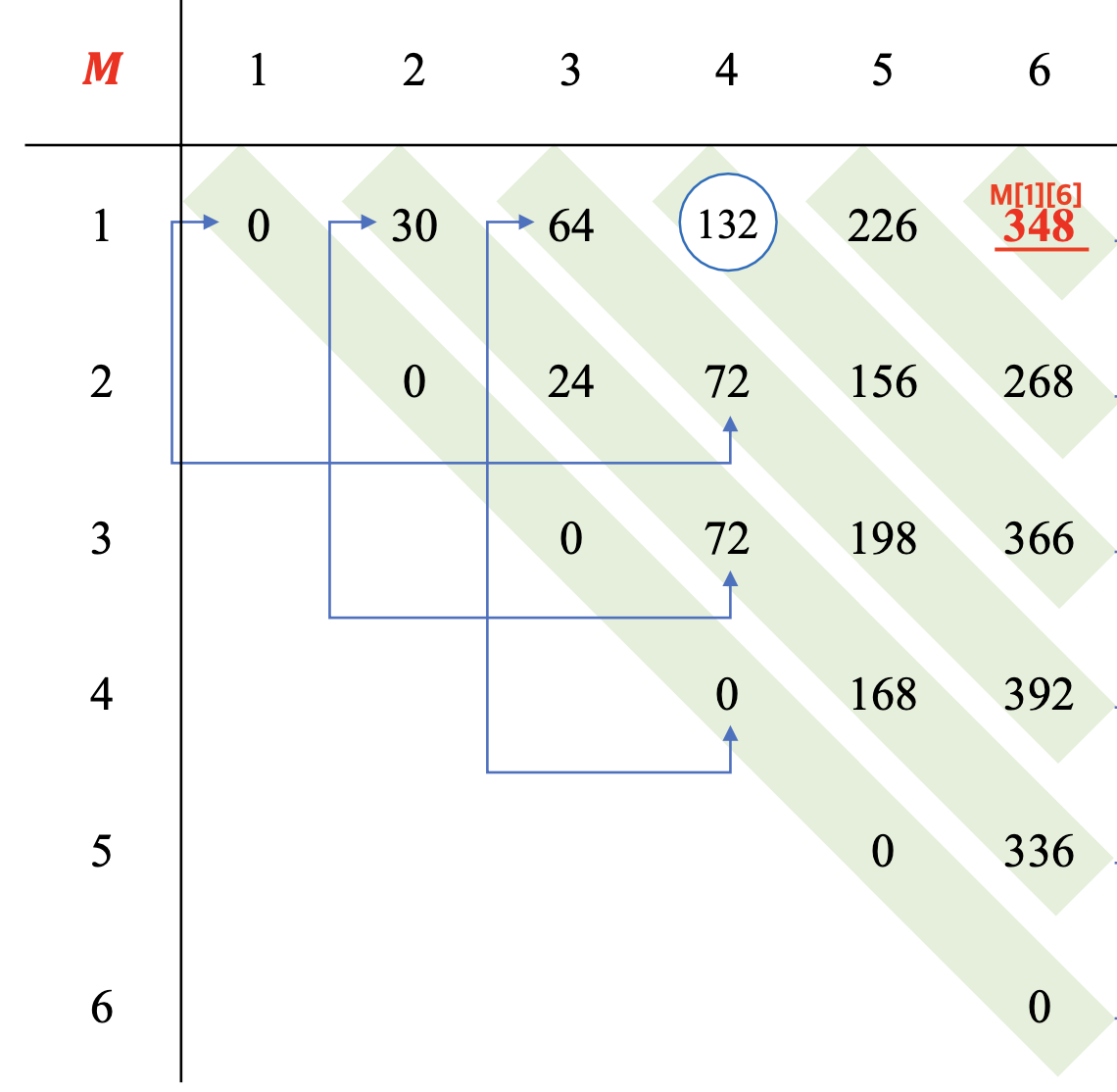
n = 6, 행렬의 크기 값 배열 d = [5, 2, 3, 4, 6 7, 8]일 때, 배열 M은 위 그림과 같다.
우리가 구하고자 하는 연쇄 행렬 곱셈의 횟수는 M[1][n]이므로, 예시의 A1부터 A6까지의 행렬 곱셈은 최소 348번이 된다는 것을 알 수 있다.
// 최솟값 구하기
int minimum(int i, int j, int& mink, vector<int>& d, matrix_t& M) {
int minValue = INF, value;
for (int k = i; k <= j - 1; k++) {
value = M[i][k] + M[k + 1][j] + d[i - 1] * d[k] * d[j];
if (minValue > value) {
minValue = value;
mink = k;
}
}
return minValue;
}
// 최소 연산 횟수 구하기
void minmult(int n, vector<int>& d, matrix_t& M, matrix_t& P) {
for (int i = 1; i <= n; i++)
M[i][i] = 0;
for (int diagonal = 1; diagonal <= n - 1; diagonal++)
for (int i = 1; i <= n - diagonal; i++) {
int j = i + diagonal, k;
M[i][j] = minimum(i, j, k, d, M);
P[i][j] = k;
}
}
시간 복잡도를 계산하면, O(n^3)이 나온다. 참고로 minmult에서 새로운 배열 P는 연쇄 행렬을 연산하는데 필요한 최소 횟수를 구하기 위해서, 분할되는 행렬 번호이다.
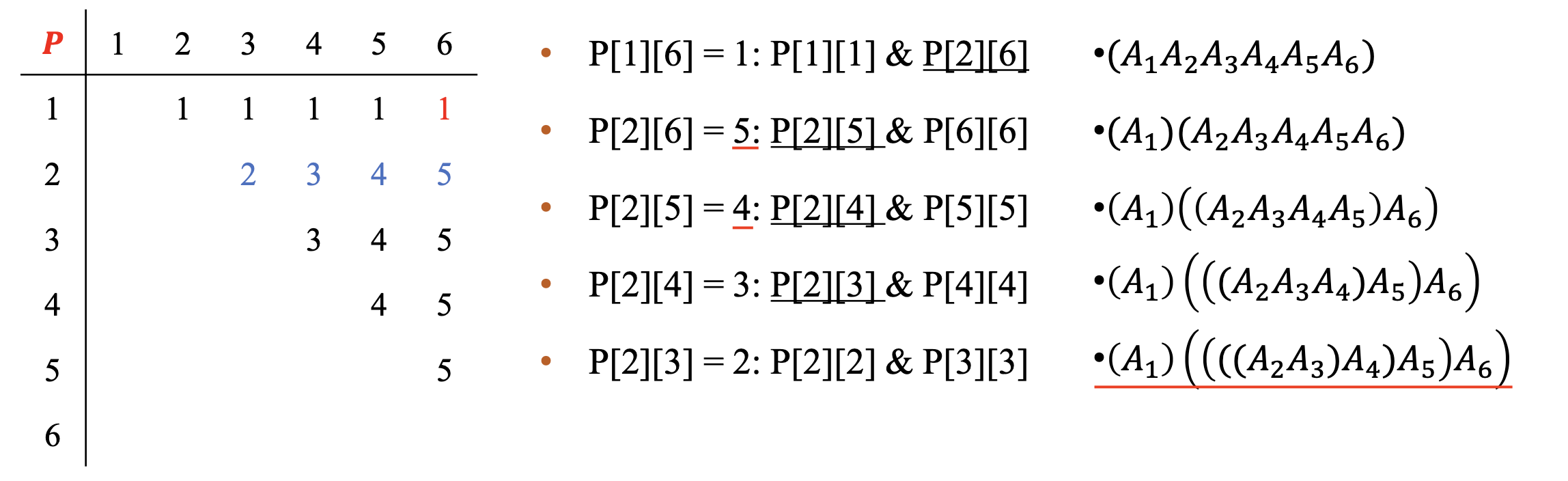
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] Knapsack Problem - Backtracking (0) | 2024.06.14 |
|---|---|
| [알고리즘] 최적 이진 탐색 트리(Optimal Binary Search Trees) (0) | 2024.04.10 |
| [알고리즘] 플로이드 알고리즘(Floyd Algorithm) (1) | 2024.04.10 |
| [알고리즘] 이항계수(The Binomial Coefficient) (0) | 2024.04.10 |
| [알고리즘] 연속 부분 수열의 합 (0) | 2022.06.20 |
