728x90
1. DAG : Directed Acyclic Graph
DAG란? 사이클이 존재하지 않는 방향 그래프
예를 들면, 라면을 끓이는 순서

어느 작업이 하나의 작업의 선행작업이 되는 경우, 자신으로 돌아올 수 없다.
👉 작업의 우선순위를 표현할 때
2. 위상정렬
- 우선순위를 표현하기 위해 사용 -> 노드들을 순서화하는 것
- 작업의 순서를 표현, 순서 유일 X
- 왼쪽에서 오른쪽으로 향하도록 한다.
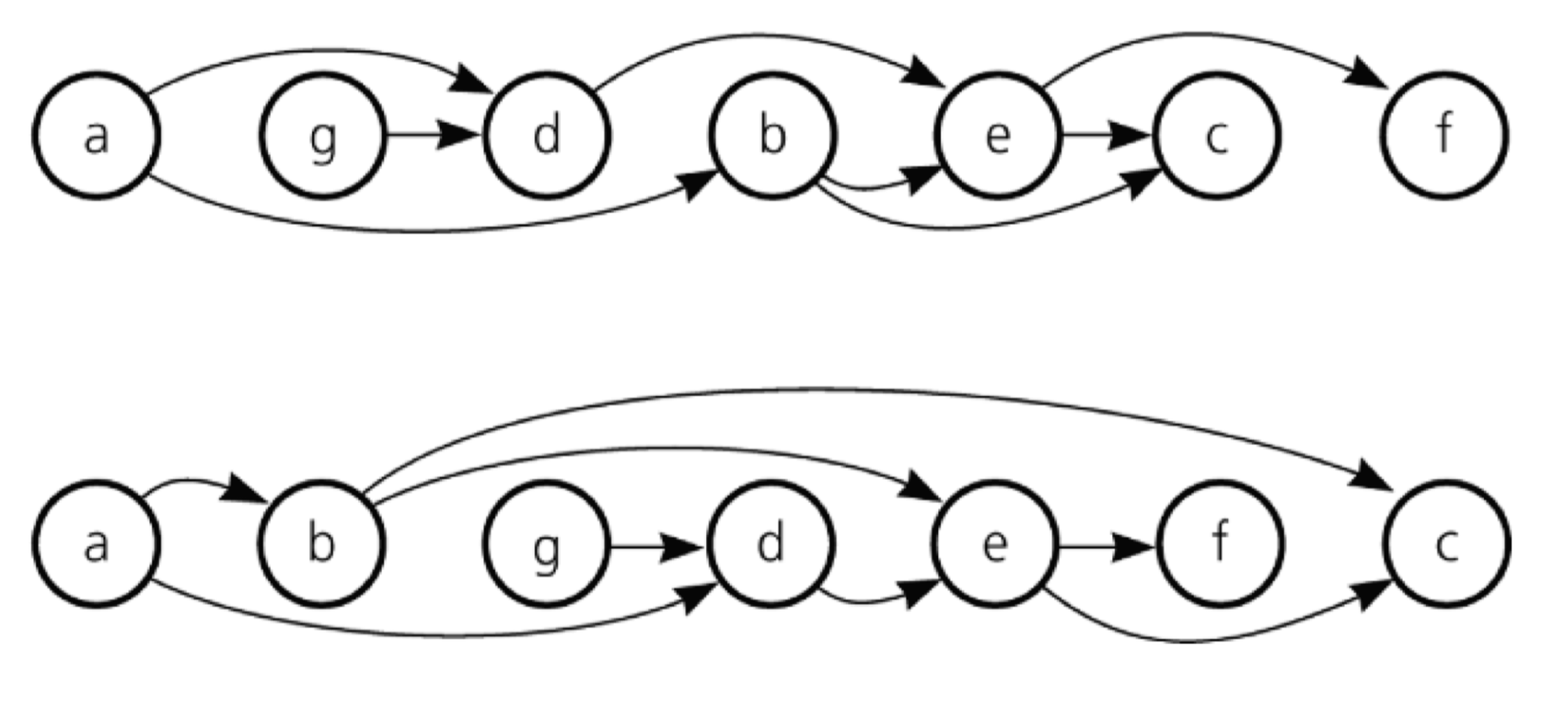
1) 위상정렬을 통한 해결 방법

- indegree(들어오는 차수)가 0인 노드를 선택한다.
-> 차수가 같다면, 어느 노드를 선택해도 무방
-> indegree가 0인 노드를 모두 큐에 삽입
2. indegree가 0인 노드 중 선택된 노드와 그 노드와 연결된 에지를 제거
-> 큐에서도 선택된 노드 삭제
3. 1~2번 과정을 반복해 모두 삭제되면 종료
2) 위상정렬 알고리즘
① 위상정렬 알고리즘 1
topologicalSort1(G) {
for <- 1 to n {
진입간선이 없는 임의 정점 u 선택
A[i] <- u;
정점 u와 u의 진출간선 모두 제거;
}
=> 배열 A[1,..,n]의 정점들이 위상정렬 되어 있음.
- indegree = 0인 노드를 선택한다. inderee가 0이라는 것은 선행작업이 없다는 의미이다.
- 노드 A와 노드 A에서 나가는 에지를 제거한다.
- 따라서 가장 먼저 나올 노드를 찾는 알고리즘으로 이해할 수 있다.
- 여기에서 indegree가 0인 간선이 없는 경우와 진출간선의 제거를 구현하는 방법을 주의해야 한다.
구현 예시이다.

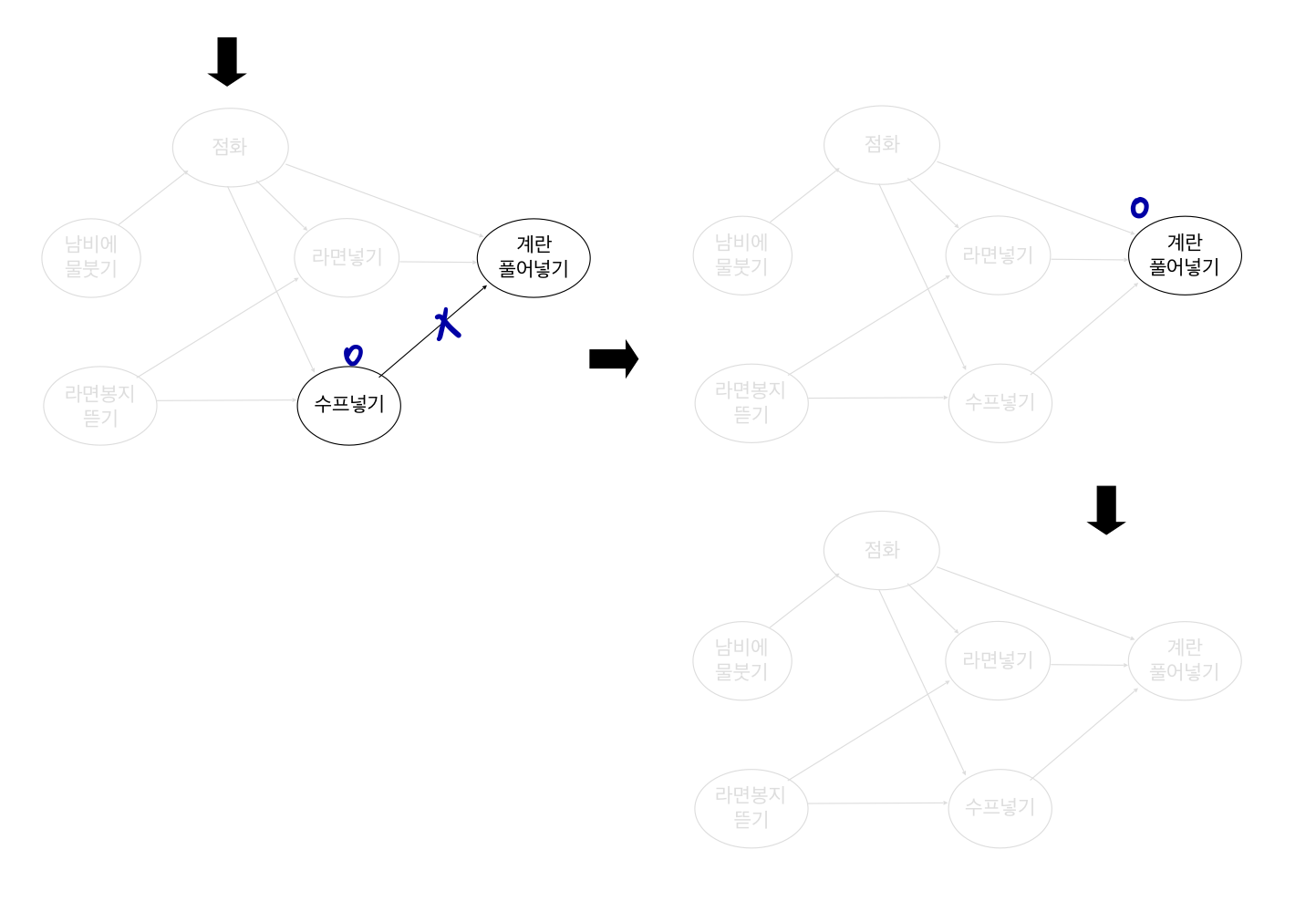
② 위상정렬 알고리즘 2
topologicalSort2(G){
for each v ∈ V
visited[v] <- NO;
make an empty linked list R;
for each v ∈ V // 정점의 순서는 상관 없음
if(visited[v] = NO) then
DFS-TS(v,R);
}
- 모든 노드들에 visited를 NO로 표시
- 위상정렬을 연결리스트에 저장하기 위해 빈 리스트를 생성한다.
- 노드의 순서에 상관없이 visited가 NO인 노드에서 다시 DFS를 반복 실행한다.
DFS-TS(v, R){
visited[v] <- YES;
for each x adjacent to v do
if(visited[x] == NO) then
DFS-TS(x,R);
add v at the front of the linked list R;
}
- 일반적인 DFS와 다른 점은 리스트에 노드 v를 추가하는 부분이다.
- 모든 노드를 방문하고 더 이상 갈 곳이 없는 경우 리스트에 추가한다
- 시간복잡도 : Θ(n+m)
- 따라서 이 알고리즘은 가장 마지막에 나올 노드를 가장 먼저 출력한다고 이해할 수 있다.



참고
(319) [알고리즘] 제14-4강 DAG - YouTube
[알고리즘] 위상 정렬(Topological Sort)이란 - Heee's Development Blog (gmlwjd9405.github.io)
728x90
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 문자열 읽고 쓰기 (0) | 2022.09.18 |
|---|---|
| [자료구조] Graph(그래프) - 최단 경로 알고리즘(벨만 포드, 다익스트라, 플로이드) (0) | 2022.06.20 |
| [자료구조] Graph(그래프) - 깊이우선순회 DFS (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 너비우선순회 BFS (0) | 2022.05.24 |
| [자료구조] Graph(그래프) - 개념과 표현 (0) | 2022.05.24 |
