728x90
1. 깊이우선순회 DFS
- 출발 노드 s에서 시작
- 현재 노드를 visited로 표시하고, 인접한 노드 중 unvisited 노드가 존재하면 노드로 향한다. (즉, leaf 노드에 도달하는 것과 같음)
- 2번을 반복
- unvisited인 이웃 노드가 존재하지 않는 동안 직전 노드로 돌아간다.
- 2번을 반복
- 출발 노드 s로 돌아오고 더 이상 갈 곳이 없으면 종료한다.
자세하게 설명하면,

1에서 시작해 unvisited인 노드 중 3을 방문한다.
다음, 3과 인접한 노드 중 unvisited 노드 7을 방문한다.
7과 인접한 노드 중 unvisited 노드 8을 방문한다.
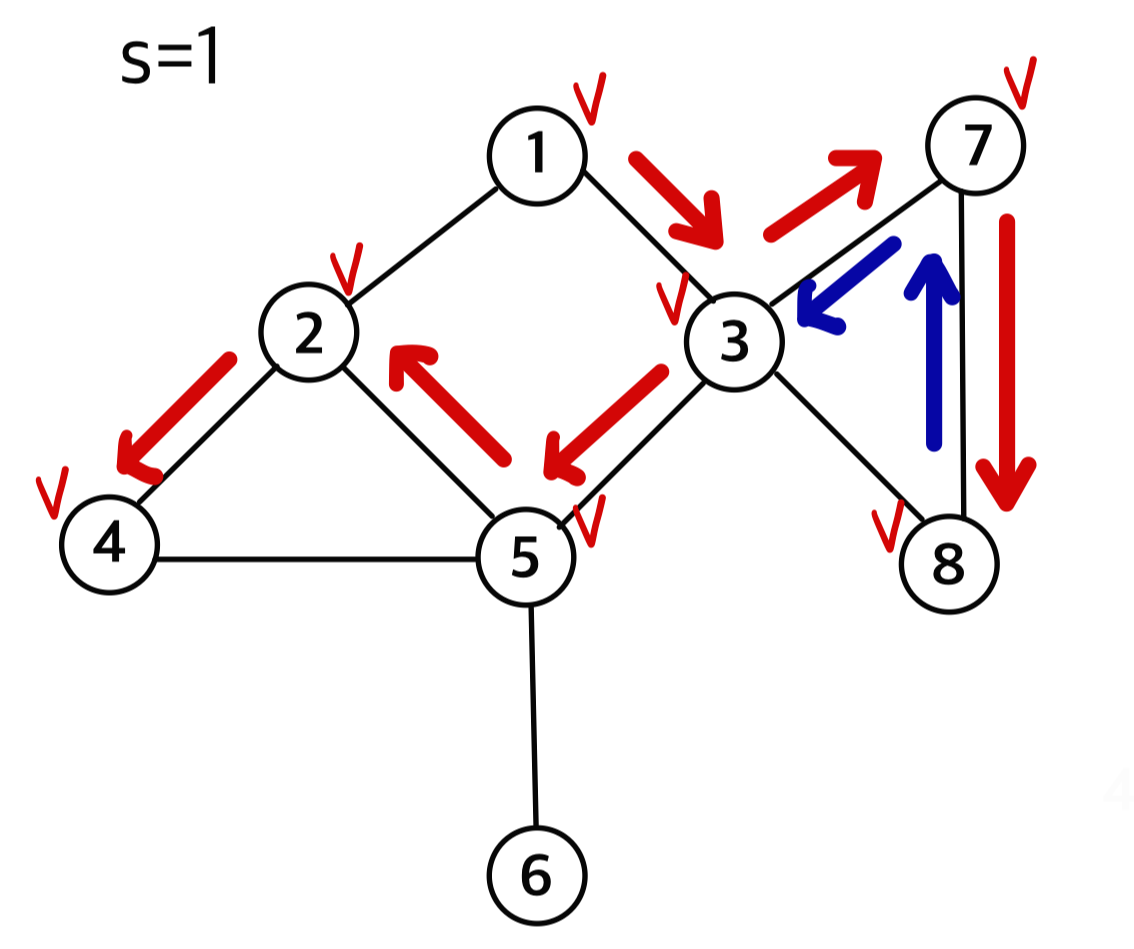
8과 인접한 unvisited인 이웃노드가 존재하지 않기 때문에 이전 노드인 7로 돌아간다.
노드 7 또한 unvisited인 이웃노드가 없으므로 이전 노드인 3으로 돌아간다.
노드 3과 인접한 노드 1은 이미 방문했으므로, unvisited 노드인 5에 방문한다.
노드 5와 인접한 unvisited 노드 2를 방문한다.
노드 2와 인접한 unvisited 노드 4를 방문한다.

노드 4와 인접한 노드 중 unvisited인 노드가 없기 때문에 직전 노드인 2로 돌아간다.
노드 2도 마찬가지로 unvisited인 노드가 없으므로 직전 노드로 돌아간다.
노드 5와 인접한 노드 중 unvisited 노드 6을 방문한다.
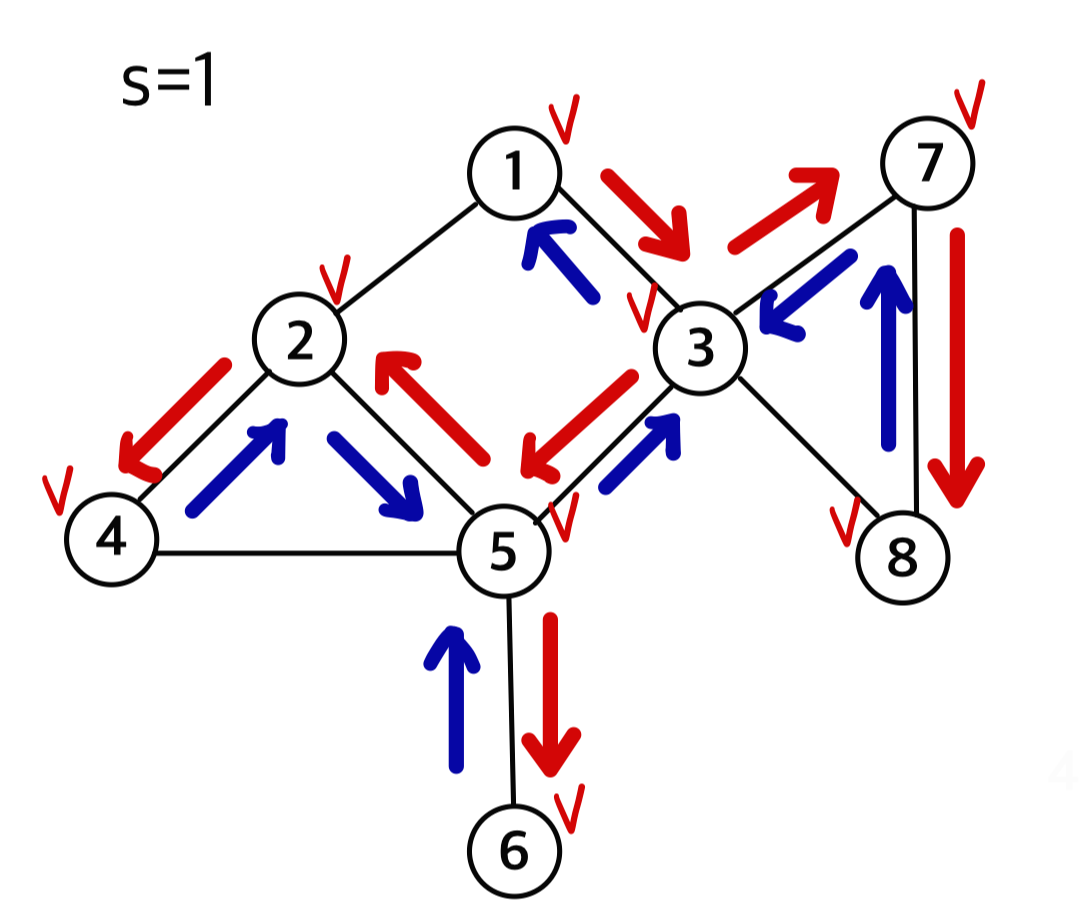
노드 6과 인접한 노드 중 unvisited인 노드가 없으므로 직전 노드인 5로 돌아간다.
노드 5도 마찬가지로 인접 노드 중 unvisited인 노드가 없으므로 직전 노드인 3으로 돌아간다.
노드 3 또한 인접노드 중 unvisited인 노드가 없으므로 직전 노드인 1로 돌아간다.
출발노드에 도착했으므로 종료
2. DFS 알고리즘
DFS(G, v)
visited[v] <- yes;
for each node u adjacent to v do
if visited[u] = NO then
DFS(G,u);
end.
end.
👉 그래프가 disconnected 이거나 방향 그래프라면 DFS에 의해 모든 노드가 방문되지 않을 수 있다.
👉 DFS를 반복하면 모든 노드를 방문 가능
DFS-ALL(G) {
for each v ∈ V
visited[v] -> NO;
for each v ∈ V
if (visited[v] = NO) then
DFS(G,v);
}
3. 시간복잡도
- 인접리스트 : O(n+m) 👉 edge 개수에 비례
- 인접행렬 : O(n^2) 👉 인접한지 모두 확인
728x90
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Graph(그래프) - 최단 경로 알고리즘(벨만 포드, 다익스트라, 플로이드) (0) | 2022.06.20 |
|---|---|
| [자료구조] Graph(그래프) - DAG (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 너비우선순회 BFS (0) | 2022.05.24 |
| [자료구조] Graph(그래프) - 개념과 표현 (0) | 2022.05.24 |
| [자료구조] 해슁(Hashing) (0) | 2022.05.20 |
