1. 그래프 순회(Graph Traversal)
순회란 ? 그래프의 모든 노드를 방문하는 일
- BFS(너비우선순회)
- DFS(깊이우선순회)
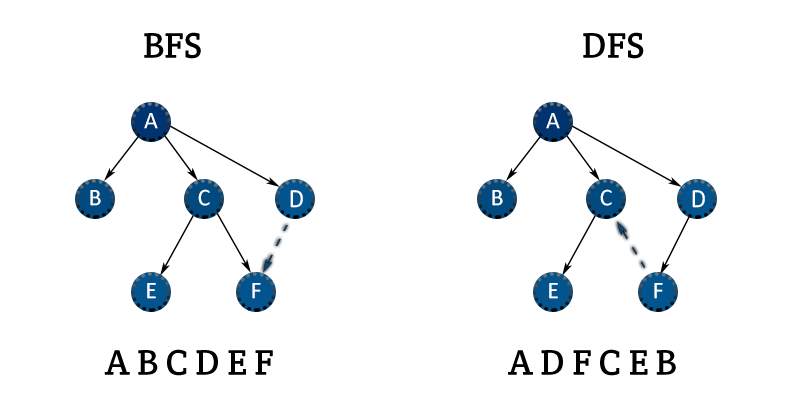
1) BFS
L0 = {s} (s : 출발노드)
L1 = L0의 모든 이웃 노드
L2 = L1의 이웃들 중 L0에 속하지 않는 노드들
.
.
Li = Li-1의 이웃들 중 Li-2에 속하지 않는 노드들
의 순서로 노드를 방문한다.
👉 level-order travasal 방식
- 큐를 이용한 너비우선순회
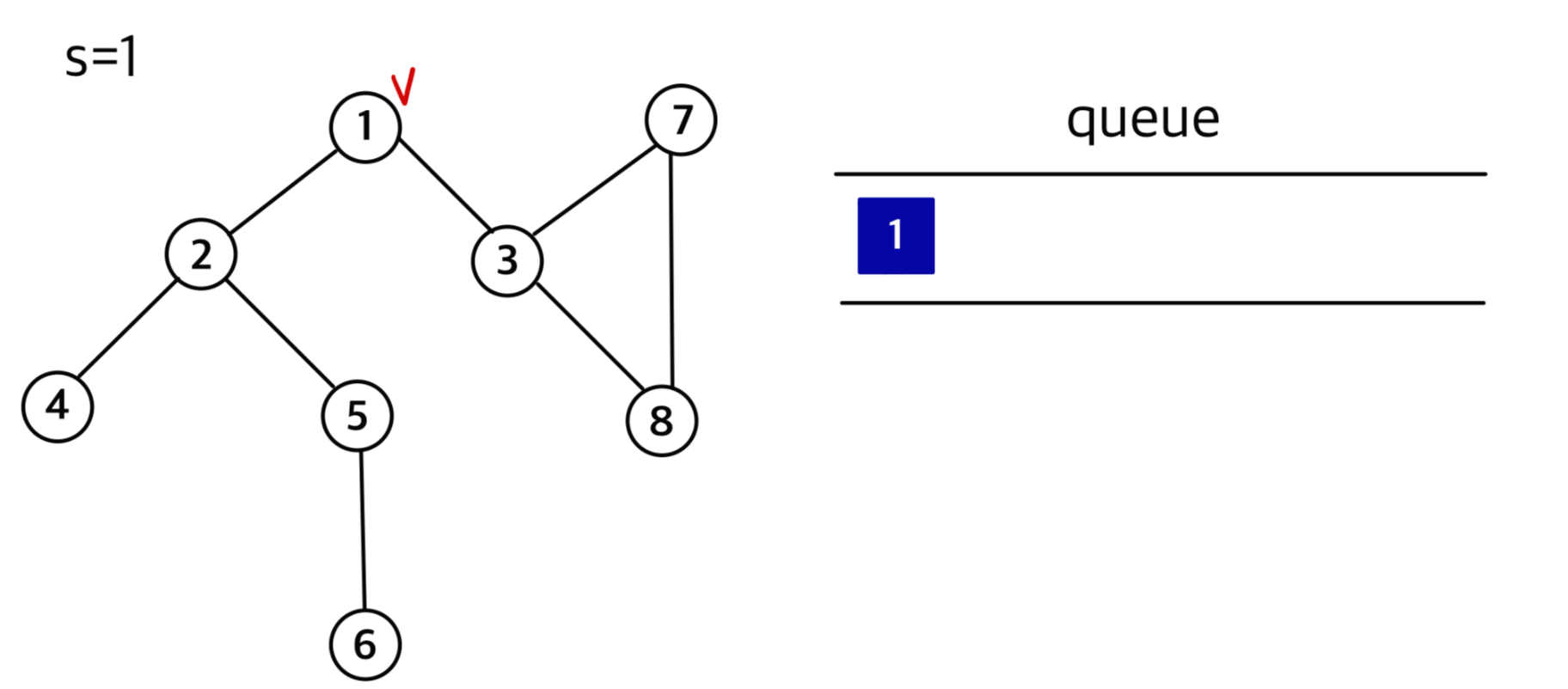
① s가 1인 노드부터 순회를 시작, 방문한 노드임을 체크 후 큐에 넣음
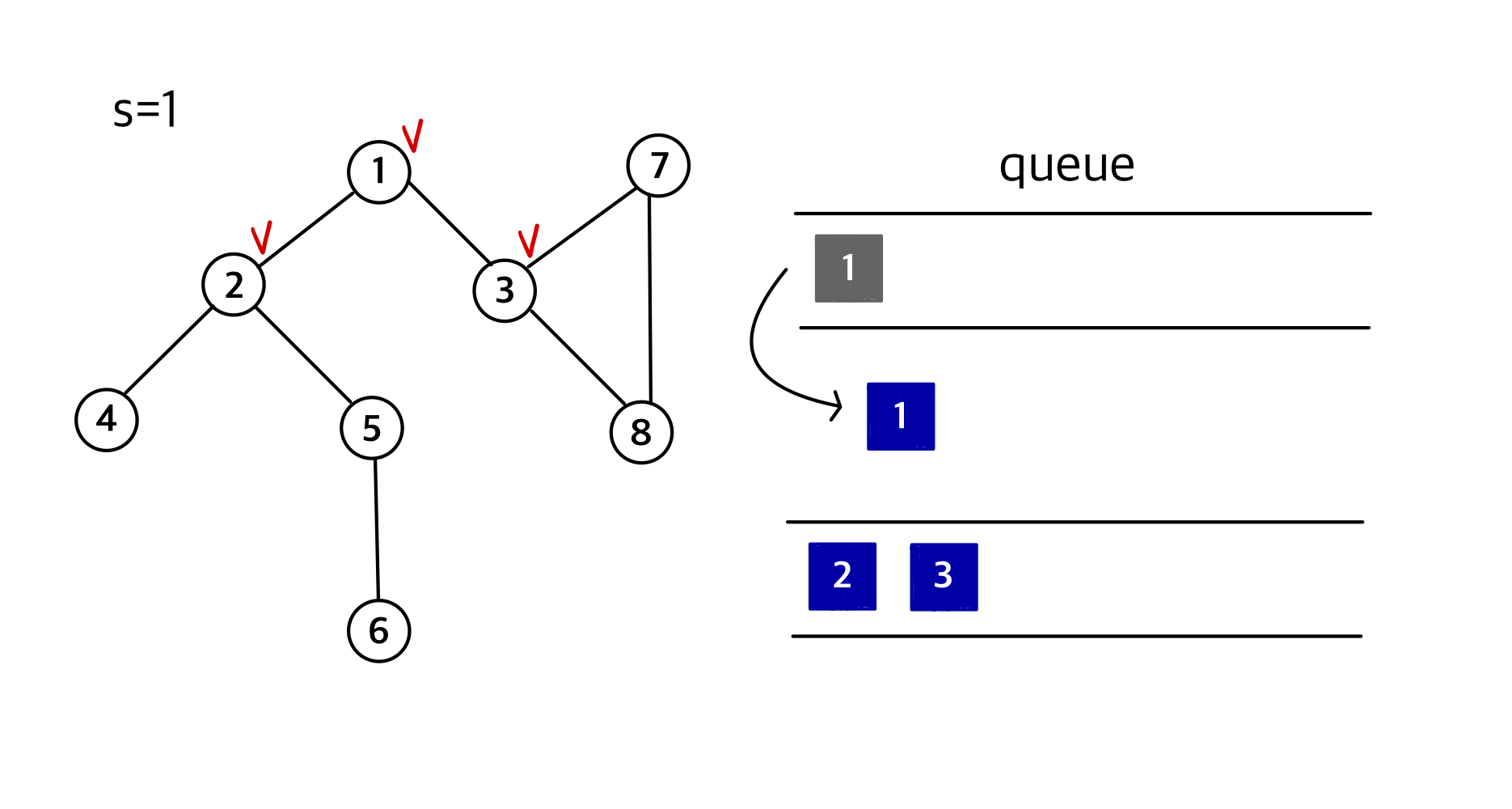
② 1을 큐에서 제거한 후 인접노드인 2, 3을 큐에 삽입

③ 2를 큐에서 제거한 후 2의 인접노드인 4, 5를 큐에 삽입
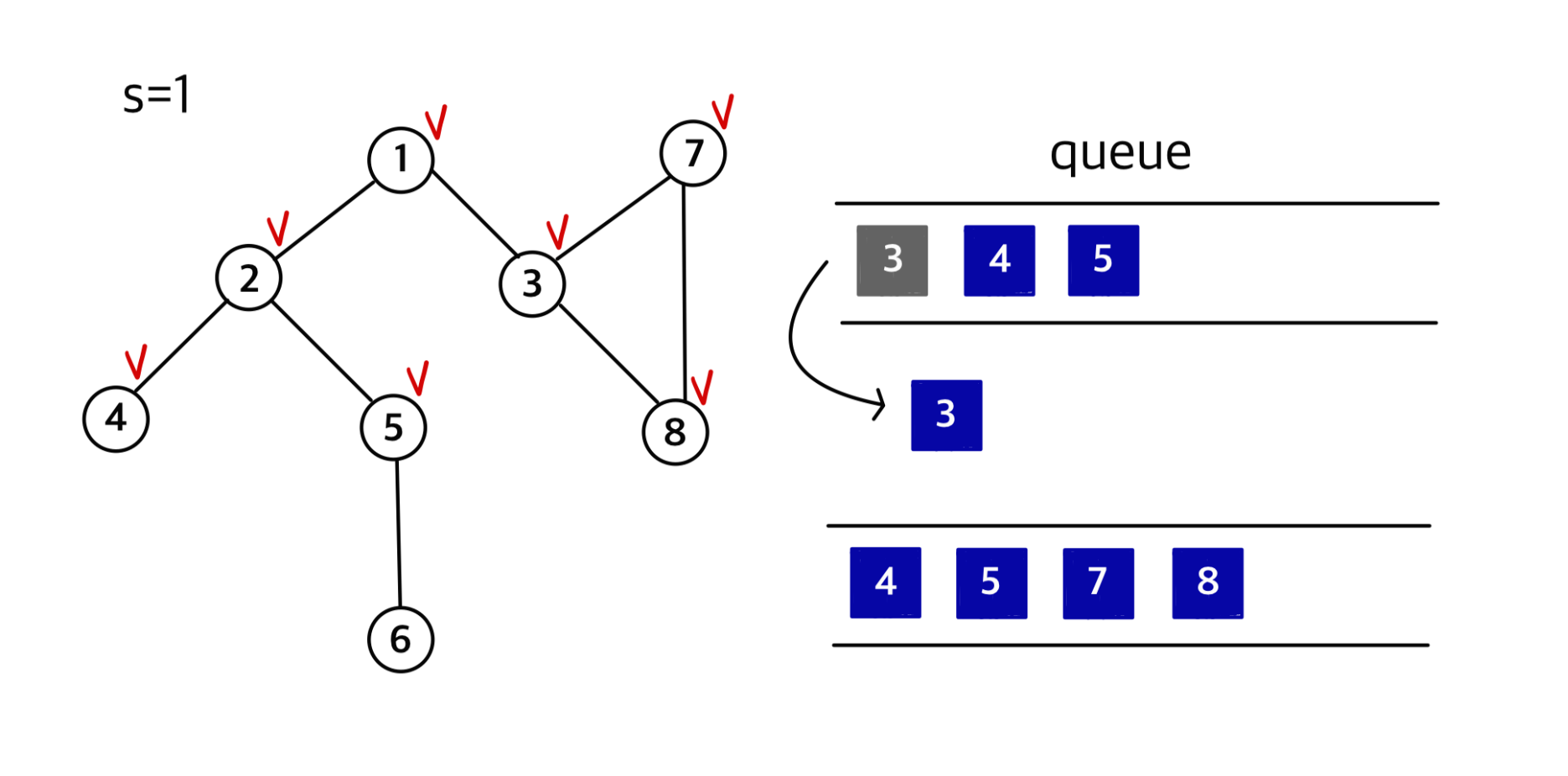
④ 3을 큐에서 제거한 후 3의 인접노드인 7, 8을 큐에 삽입

⑤ 4를 큐에서 제거, 4의 인접노드인 2와 5는 이미 방문한 노드이므로 pass

⑥ 5를 큐에서 제거한 후 5의 인접노드인 6을 큐에 삽입
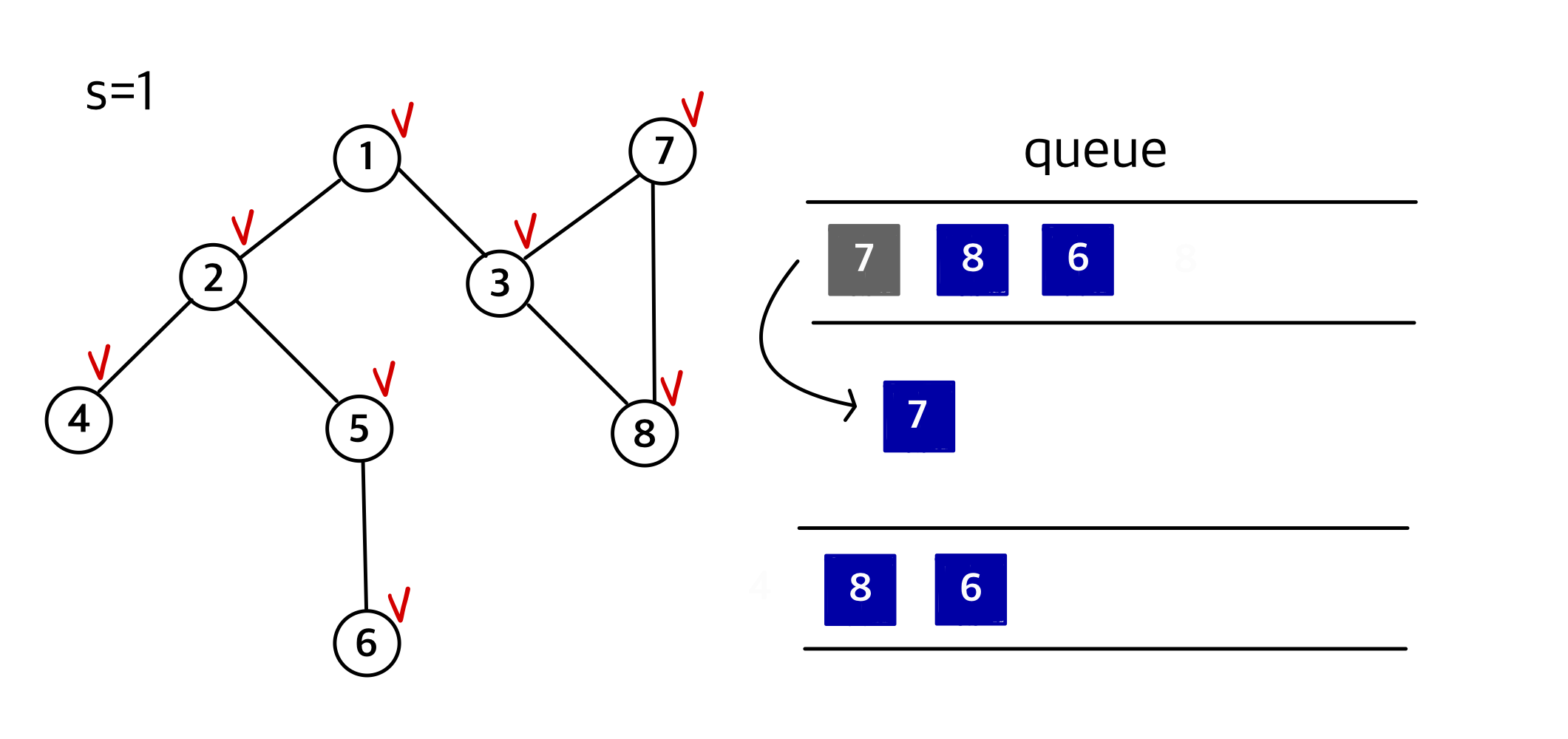

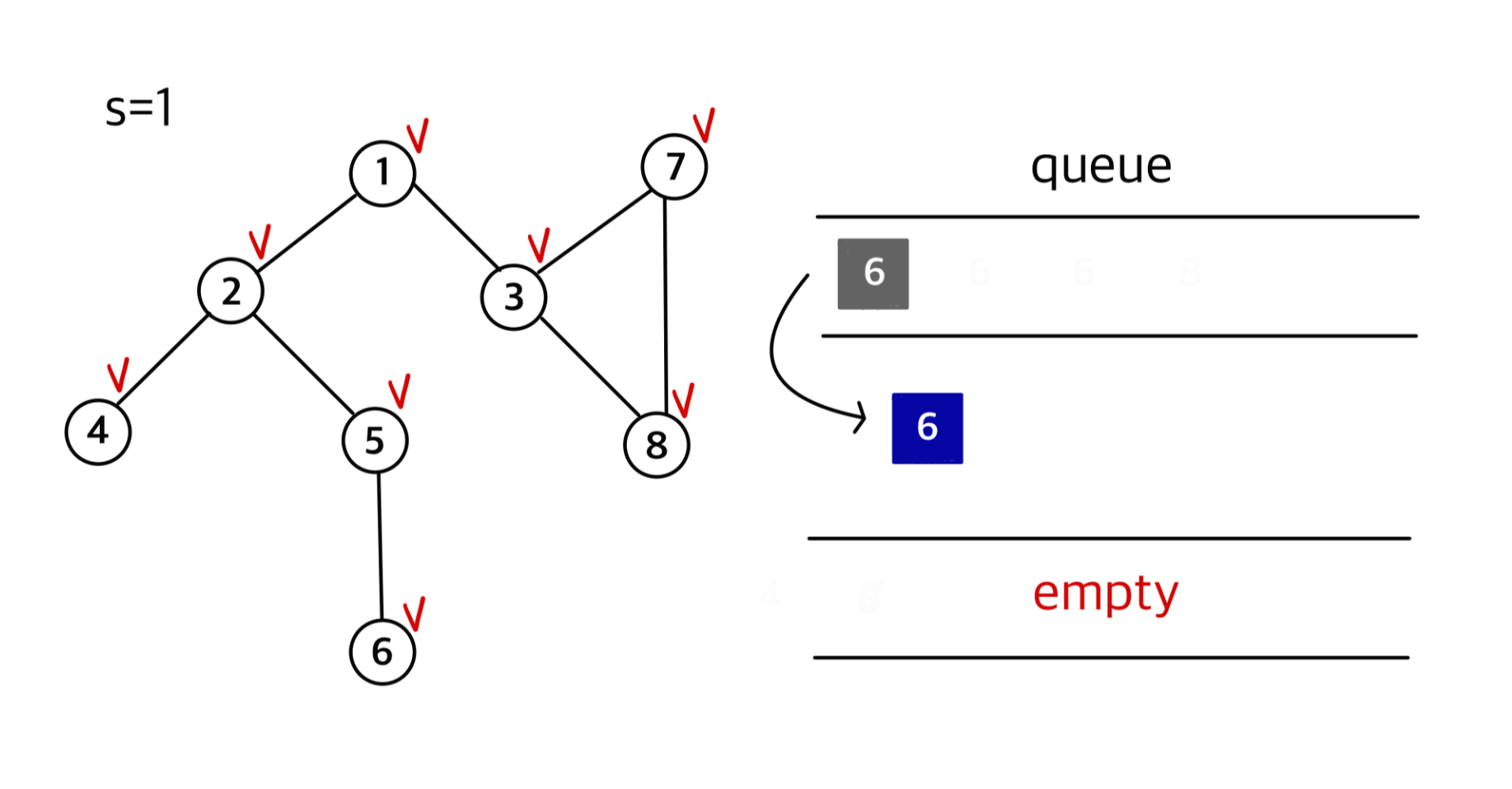
⑦ 차례로 7, 8, 6을 큐에서 제거
👉노드방문순서 : 1, 2, 3, 4, 5, 7, 8, 6 (유일하지 않음)
수도 코드는 다음과 같다.
BFS(G,s)
Q<-Ø;
Enqueue(Q,s);
while Q≠Ø do
u <- Dequeue(Q)
for each v adjacent to u do
if v is unvisited then
mark v as visited;
Enqueue(Q,v);
end.
end.
end.
위를 바탕으로 작성한 파이썬 코드는 다음과 같다.
from collections import deque
def bfs(graph, start, visited):
queue=deque([start])
visited[start]=True
while queue:
v=queue.popleft()
print(v,end='')
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i]=True
graph=[
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
visited=[False]*9
bfs(graph, 1, visited)
2. BFS와 최단경로
˙ s에서 Li에 속한 노드까지의 최단 경로의 길이는 i, 경로의 길이는 경로에 속한 에지 수를 뜻함
˙ 입력 : 방향/무방향 그래프 G=(V,E), s∈V
˙ 출력 : 모든 노드 v에 대해
d[v] = s에서 v까지의 최단경로의 길이
<코드 추가 예정>
- 인접행렬 : O(n^2)
- 인접리스트 : O(n+m)
3. BFS 트리 : 각 노드 v와 π[v]를 연결하는 edge로 구성된 트리
˙ s에서 v까지의 경로는 s에서 v까지의 최단 경로
˙ 어떤 edge도 2개의 layer을 건너가지 않는다.

PRINT-PATH(G,s,v) /* 출발점 s에서 노드 v까지의 경로 출력하기 */
if v=s then
print s;
else if π[v]=null then
print "no path from s to v exists";
else
PRINT-PATH(G,s,π[v]);
print v;
end.
* 그래프가 disconnected 이거나 방향 그래프라면 모든 노드가 방문되지 않을 수 있음.
👉 BFS를 반복해 모든 노드를 반복하게 만들어 주어야 함.
BFS-ALL(G) {
while there exists unvisited node v
BFS(G,v)
}
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Graph(그래프) - 최단 경로 알고리즘(벨만 포드, 다익스트라, 플로이드) (0) | 2022.06.20 |
|---|---|
| [자료구조] Graph(그래프) - DAG (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 깊이우선순회 DFS (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 개념과 표현 (0) | 2022.05.24 |
| [자료구조] 해슁(Hashing) (0) | 2022.05.20 |
