1. 그래프의 개념
그래프 G는 두 개의 집합 V와 E로 구성
- V : node 혹은 vertex
- E : node 쌍을 연결하는 edge
-> V(G)와 E(G)는 그래프 G의 정점들의 집합과 간선들의 집합을 나타냄.
-> 개체들 간의 이진관계 표현
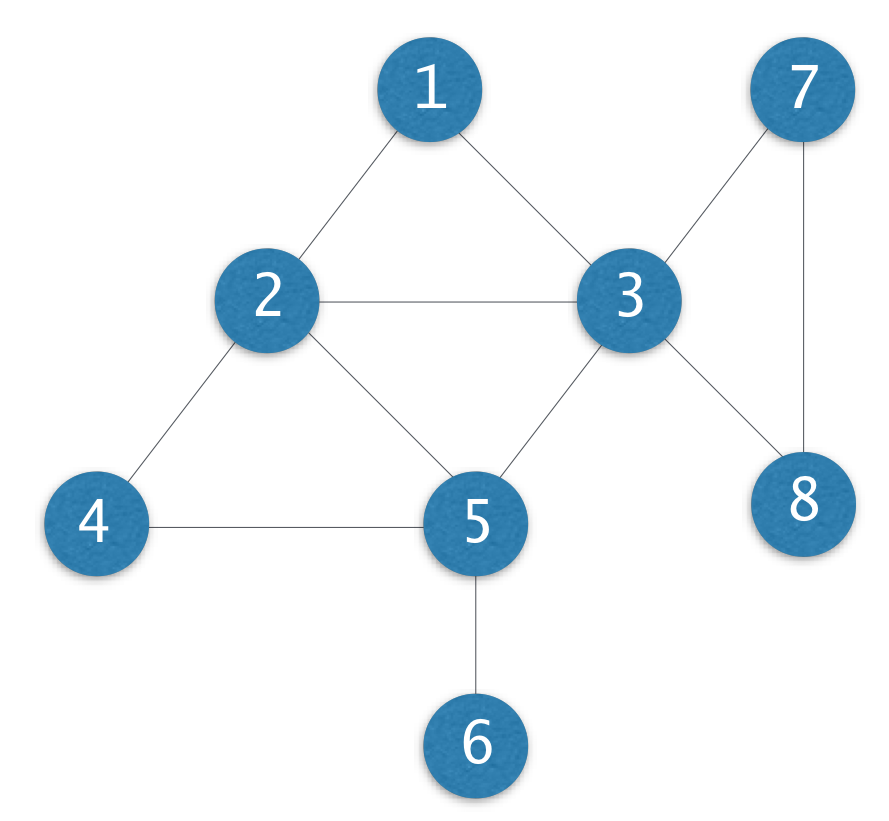
V = {1,2,3,4,5,6,7,8}
E = {(1,2), (1,3), (2,3), .. , (7,8)}
n = |V| = 8
m = |E| = 11
그래프의 종류에는 2가지가 있다.
- 방향그래프(Directed Graph) G = (V,E) : edge (u,v)는 u->v
- 가중치 그래프(Weighted Graph) : edge 마다 가중치 지정
2. 그래프의 표현
* 무방향 그래프
1) 인접행렬 (adjacency matrix) : n x n 행렬 A = a[i][j]
- 간선 (i, j)가 E(G)에 속하면 a[i][j] = 1, 속하지 않으면 a[i][j] = 0
- 무방향 그래프에서는 인접행렬이 대칭, 방향 그래프에서는 대칭이 아닐 수 있음.
👉 저장공간 O(n^2)
👉 어떤 node v에 인접한 모든 노드 찾기 : O(n) 시간
👉 어떤 edge (u,v)가 존재하는지 검사 : O(1) 시간
2) 인접리스트 (adjacency list)
- 정점 집합을 표현하는 하나의 배열과 각 정점마다 인접한 정점들의 연결 리스트

- n개의 정점과 e개의 간선을 갖는 그래프에 대한 인접리스트 표현 : 크기가 n인 배열과 2e개 체인노드
👉 저장공간 O(n+e)
👉 어떤 node v에 인접한 모든 노드 찾기 : O(degree(v)) <- 연결리스트의 길이에 비례
👉 어떤 edge (u,v)가 존재하는지 검사 : O(degree(u))
* 방향그래프
1) 인접행렬 (adjacency matrix) : 비대칭
2) 인접리스트 (adjacency list) : m개의 노드
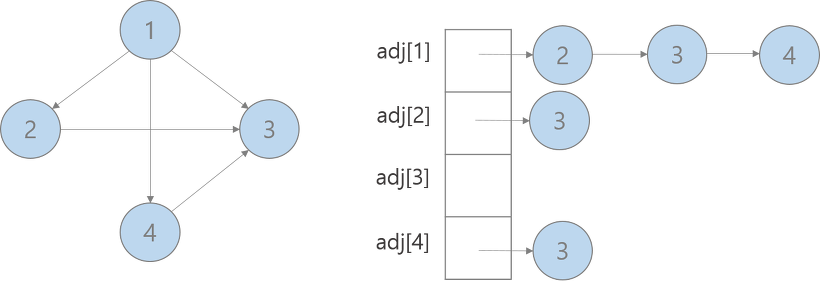
- 리스트 노드의 수는 e개
- 정점의 진출 차수 = 해당 정점의 인접리스트의 노드 수
* 가중치그래프
1) 인접행렬 (adjacency matrix)
- edge의 존재를 나타내는 값으로 edge의 가중치 저장
- edge가 없거나 대각선인 경우 : 특별히 정해진 규칙은 없지만 그래프와 가중치가 의미하는 바에 따라 다름.
ex) 가중치가 거리나 비용을 의미 : edge가 없을 때는 ∞, 대각선의 경우 0
가중치가 용량을 의미 : edge가 없을 때는 0, 대각선의 경우 ∞
- 경로와 연결성
- 무방향 그래프 G = (V,E)에서 노드 u와 노드 v를 연결하는 경로가 존재할 때 v와 u는 연결되었다고 말함.
- 즉, Connected Graph를 말하는 것.
- 연결요소 (Connected Component)
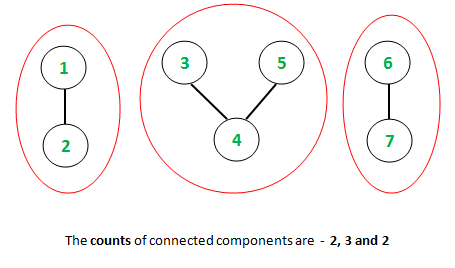
** 인접(adjacent) : (u,v)가 E(G)의 한 간선일 때 u와 v는 인접한다고 말함.
참고자료
https://velog.io/@stat_wkon/TIL-2-BFS%EC%99%80-DFS-%EC%9D%B4%ED%95%B4
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Graph(그래프) - 최단 경로 알고리즘(벨만 포드, 다익스트라, 플로이드) (0) | 2022.06.20 |
|---|---|
| [자료구조] Graph(그래프) - DAG (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 깊이우선순회 DFS (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 너비우선순회 BFS (0) | 2022.05.24 |
| [자료구조] 해슁(Hashing) (0) | 2022.05.20 |
