1. 해쉬테이블
- dynamic set을 구현하는 효과적 방법 중 하나
- 평균 탐색, 삽입, 삭제 시간은 O(1)
- 최악의 경우 Θ(n)

- 해쉬함수 h를 이용해 키 k를 T[h(k)]에 저장
- h : U -> {0, 1, ..., m-1} (m : 테이블 크기, U : 모든 가능한 키들의 집합)
- 하나의 slot 혹은 bucket으로 사상됨
- 즉, 각 키는 0 ~ m-1의 정수로 mapping
2. 해쉬 함수의 예
- 모든 키를 자연수로 가정
예1) 문자열
ASCII 코드 : C = 67, L = 76, R = 82, S = 83
CLRS = (67 * 128^3) + (76 * 128^2) + (82 * 128^1) + 83 * (128^0)
예2) h(k) = k % m : key를 m으로 나눈 나머지
3. 충돌(Collision)
=> 서로 다른 키가 동일한 slot에 사상된다면?
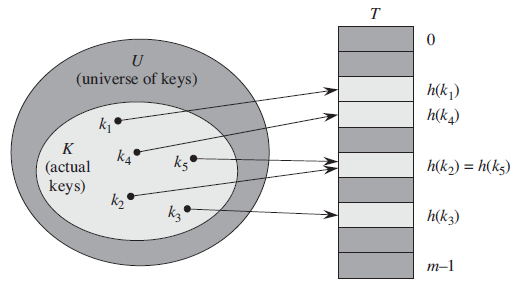
- 서로 다른 키 k1, k2가 h(k1) = h(k2) 인 경우 즉, 해시값이 동일한 경우
- 정의 구역의 크기가 테이블 크기보다 크기 때문에 항상 발생 가능(단사함수 X)
** 단사함수가 되려면?
: 집합 A의 크기가 U보다 커야함. 즉, 테이블 크기 m이 U보다 크거나 같아야 함.
- 실제로 저장된 키들의 집합 A가 테이블 크기 m보다 큰 경우엔 당연히 발생
=> chaining / open addressing 으로 해결 가능
* 충돌을 해결하는 방법
1) Open Hashing
- Chaining
2) Closed Hasing
- Chaining(open hashing이면서 closed hashing)
- Open addressing
· linear probing
· quardratic probing
· double hashing
1) chaining
: 동일한 slot 으로 해슁된 모든 키를 하나의 연결리스트로 저장
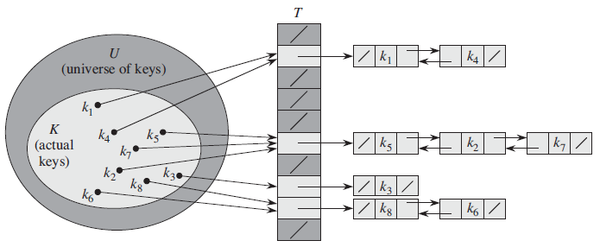
① insert
- 키 k를 리스트 T[h(k)]의 맨 앞에 삽입 : 시간복잡도 O(1)
- 중복 저장이 허용되지 않으면, 삽입 시 리스트를 검색해야 함. => 시간복잡도 ∝ 리스트 길이
② search
- 리스트 T[h(k)]에서 순차검색 => 시간복잡도 ∝ 리스트 길이
③ delet
- 리스트 T[h(k)] 로부터 키를 검색 후 삭제
- 키를 검색해서 찾은 후에는 O(1)에 삭제 가능
- 최악의 경우 : 모든 키가 하나의 slot으로 해슁되는 경우
· 길이가 n인 연결리스트, 탐색시간은 Θ(n) + 해쉬함수 계산시간
- 평균시간복잡도 : 여러 slot에 얼마나 잘 분배되는지에 따라 결정
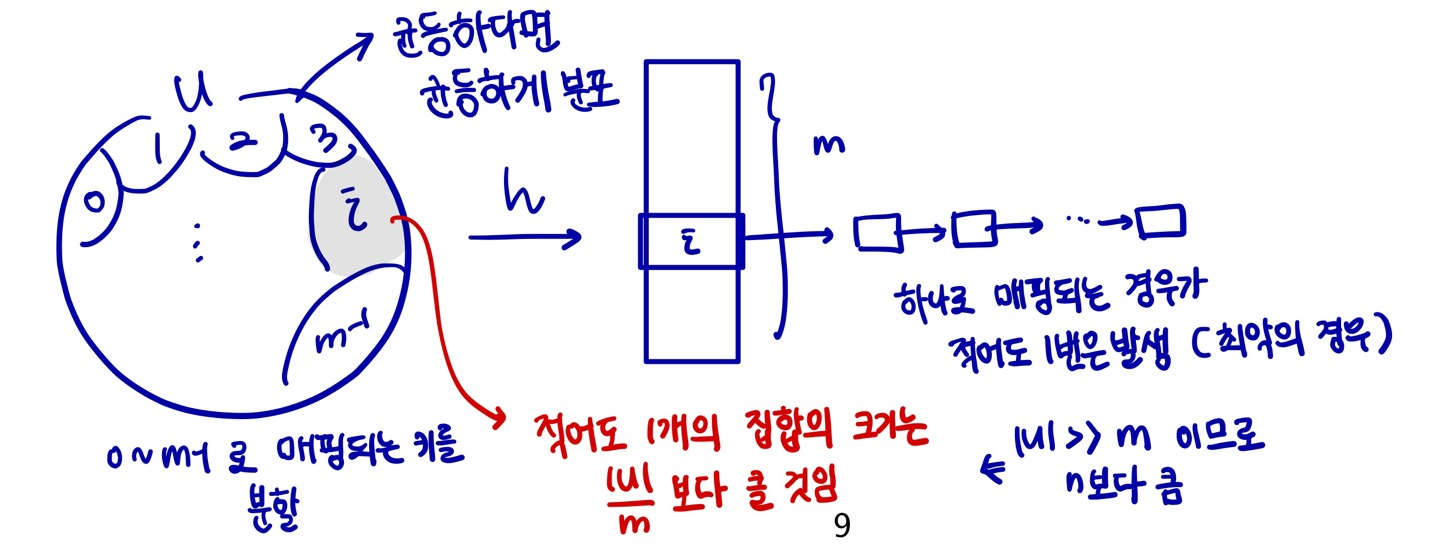
* SUHA(Simple Uniform Hashing Assumption)
- 각각의 키가 모든 slot에 균등한 확률로 독립적으로 해슁된다는 가정(성능분석을 위함)
-> hash 함수는 deterministic 하므로 현실에서 불가
- Load Factor α = n / m
· n : 테이블에 저장될 키 개수
· m : 해쉬테이블의 크기(연결리스트 개수)
· 각 slot 에 저장된 키의 평균 개수
· 연결리스트 T[j]의 길이를 nj 라고 할 때 E[nj] = α (한 slot으로 배분될 key의 기댓값)
2) open addressing
: 모든 키를 해쉬 테이블 자체에 저장, 테이블 각 slot에는 1개의 키만 저장
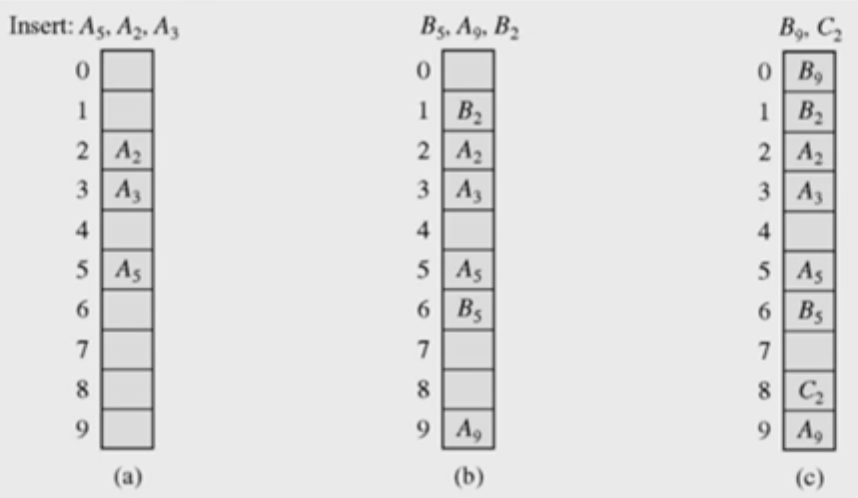
① linear probing

- h(k), h(k)+1, h(k)+2,.. 순서로 검사해 처음으로 빈 slot에 저장
- 테이블의 끝이 도달하면 처음으로 circular
- (b) : B5와 A5의 충돌 => 그 다음 slot이 비었으면 저장, 아니라면 다음 slot 이 비었는지 탐색
- (c) : C2와 A2의 충돌 => 최초로 빈 slot이 나올 때까지 탐색
B9와 A9의 충돌 => 테이블의 끝이므로 circular
- 단점
· primary cluster : 키에 의해 채워진 연속된 slot. 즉, 키들이 뭉쳐진 상태
· 클러스터링이 점점 더 커지는 경향 => 원래 저장되어야 할 곳보다 더 먼 곳에 저장. 검색시간 ∝ cluster 길이
/* h(x) 계산 */
/* T[h(k)], T[(h(k)+1)%b], .. , T[(h(k)+j)%b]의 순서로 slot 탐색
1) T[(h(k)+j)%b]에 값이 k인 키 쌍이 있는 경우
=> 원하는 쌍이 발견됨
2) T[h(k)+j]이 비어있는 경우
=> k는 테이블에 존재하지 않음
3) 시작 위치 T[h(k)]에 돌아온 경우
=> 테이블은 꽉 찼고, k는 테이블에 존재하지 않음
*/// 포인터 사용
#include <stdio.h>
int main() {
// 선형 조사법 해시 테이블 T에서 k 탐색
// 이 키를 가진 쌍을 발견하면 포인터 반환
// 그렇지 않으면 0
int i = h(k) // 홈 버킷
int j;
for (j = i; T[j] && T[j] -> first != k;) {
j = ( j + 1 ) % b; // 테이블을 원형으로 간주
if (j==i) // 시작점으로 복구
return 0;
}
if (T[j]->first == k)
return T[j];
return 0;
}
② Quadratic probing
: 검색에 필요한 탐색의 평균 횟수를 줄이는 방법
- 충돌 발생시 h(k), h(k)+1^2, h(k)+2^2, h(k)+3^2, ... 순서로 시도
- B2와 A2의 충돌 => h(B2) + 1^2, h(B2) + 2^2, h(B2) + 3^2 순서로 탐색
- C2와 A2의 충돌 => h(C2) + 1^2, h(C2) + 2^2, h(C2) + 3^2, h(C2) + 4^2 순서로 탐색
- 모든 키에 대한 offset이 동일
③ double hashing

- 클러스터링이 발생하지 않도록 하는 과정
- (h1(k) + i * h2(k)) mod m
- h1(14) = 1, h2(14) = 4 => offset = 4
- h1(15) = 2, h2(15) = 5 => offset = 5
* open addressing 의 단점
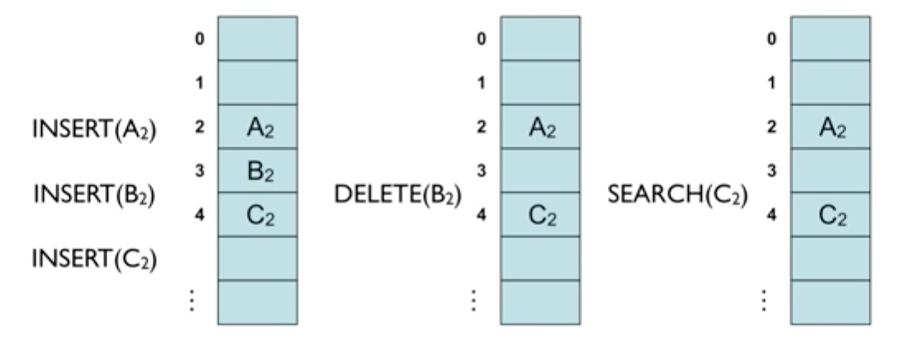
- 키를 삭제할 때 문제 발생
- A2, B2, C2가 동일한 해쉬함수값을 가져서 linear probing으로 해결한 후 B2 삭제, C2 검색
- 중간의 B2가 삭제되었기 때문에 C2까지 닿지 못함
- B2를 삭제한 후 C2를 삭제된 B2 자리에 놓아야 함. 즉, 삭제한 후 각 키들을 한 자리씩 이동해야함
* 좋은 해쉬 함수?
- 현실에서는 키가 랜덤하지 않는다.
- 키들이 특정한 패턴을 가지더라도 해쉬함수값이 불규칙적이 되도록 하는 것이 바람직
- 즉, 해쉬함수값이 키의 특정부분에 의해서만 결정되지 않아야 한다.
4. 해쉬함수
1) division 기법
- h(k) = k mod m
- 장점 : 한번의 mod 연산으로 계산하기 때문에 빠르다.
- 단점: 어떤 m 값에 대해서는 해쉬함수값이 키의 특정 부분에 의해 결정된다.
예를 들면, m = 2^p 일 때, 키의 하위 p비트가 해쉬함수값이 된다.
2) multiplication 기법
- 0~1 사이의 상수 a
- ka의 소수부분만 선택해 m을 곱한 후 소수점 아래를 버림
- 두 키가 유사하거나 공통점이 있다고 해도 최종적인 값을 예측하기 어렵다.
참고자료
https://new93helloworld.tistory.com/147
http://egloos.zum.com/itfs/v/9984604
https://www.fun-coding.org/Chapter09-hashtable.html
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Graph(그래프) - 최단 경로 알고리즘(벨만 포드, 다익스트라, 플로이드) (0) | 2022.06.20 |
|---|---|
| [자료구조] Graph(그래프) - DAG (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 깊이우선순회 DFS (0) | 2022.06.02 |
| [자료구조] Graph(그래프) - 너비우선순회 BFS (0) | 2022.05.24 |
| [자료구조] Graph(그래프) - 개념과 표현 (0) | 2022.05.24 |
