728x90
최단 경로 알고리즘은 대표적으로 다익스트라와 플로이드 알고리즘이 있다.
- Dijkstra : 어떤 정점부터 다른 모든 정점까지의 최단 경로를 구하는 알고리즘
- Floyd : 그래프에 존재하는 모든 정점 사이의 최단 경로를 한번에 구하는 알고리즘
1. 다익스트라 알고리즘
- 집합 S : 최단 경로가 이미 발견된 정점들의 집합
- 1차원 배열 distance : 집합 S에 있는 정점만을 거쳐서 다른 정점으로 가는 최단 거리를 저장하는 배열, 해당 정점 간의 가중치가 저장
- 인접 행렬 weight : 가중치를 저장하는 행렬
다익스트라의 원리는 다음과 같다.
매 단계마다 집합 S에 속하지 않는 정점 중에서 distance 값이 가장 작은 정점들을 추가해 나간다.
새로운 정점이 S에 추가되면 S에 속하지 않는 정점들의 distance 값을 수정한다.
새로 추가된 정점을 거쳐서 정점까지 가는 거리와 기존의 거리를 비교해 더 작은 값으로 distance를 수정한다.
1) 예제 그래프에서 초기값은 다음과 같다. 위에 그려진 배열이 distance 이다.

2) distance 값이 가장 작은 정점을 선택한다. 이 정점에 간선이 생기면서 변화하는 가중치 값을 수정한다.
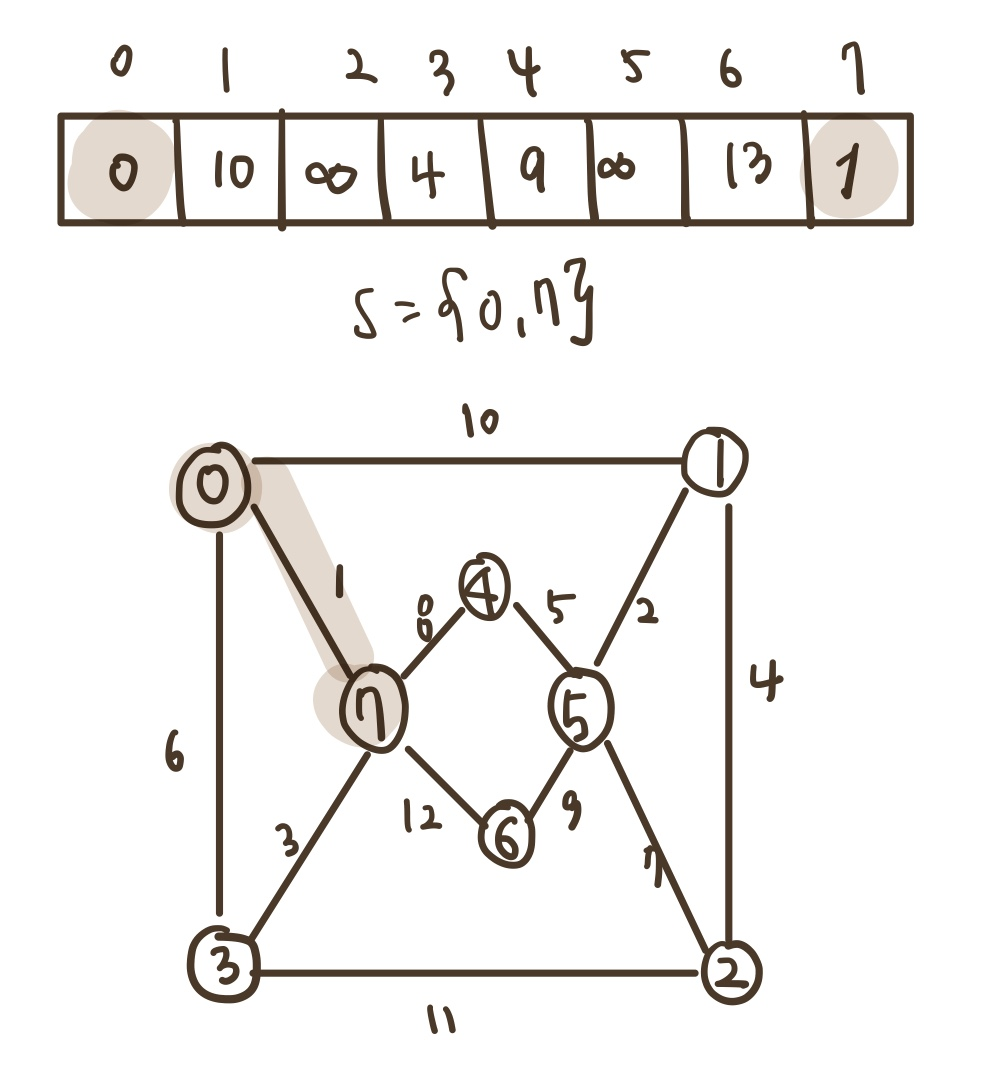
distance[0] = 0
distance[1] = min(distance[1], distance[7] + weight[7][1]) = min(10, ∞) = 10
distance[2] = min(distance[2], distance[7] + weight[7][2]) = min(∞, ∞) = ∞
distance[3] = min(distance[3], distance[7] + weight[7][3]) = min(6, 4) = 4
distance[4] = min(distance[4], distance[7] + weight[7][4]) = min(∞, 9) = 9
distance[5] = min(distance[5], distance[7] + weight[7][5]) = min(∞, ∞) = ∞
distance[6] = min(distance[6], distance[7] + weight[7][6]) = min(∞, 13) = 13
distance[7] = 1
3) 배열에서 가중치가 가장 작은 3을 선택하고 다른 가중치 값을 수정한다.
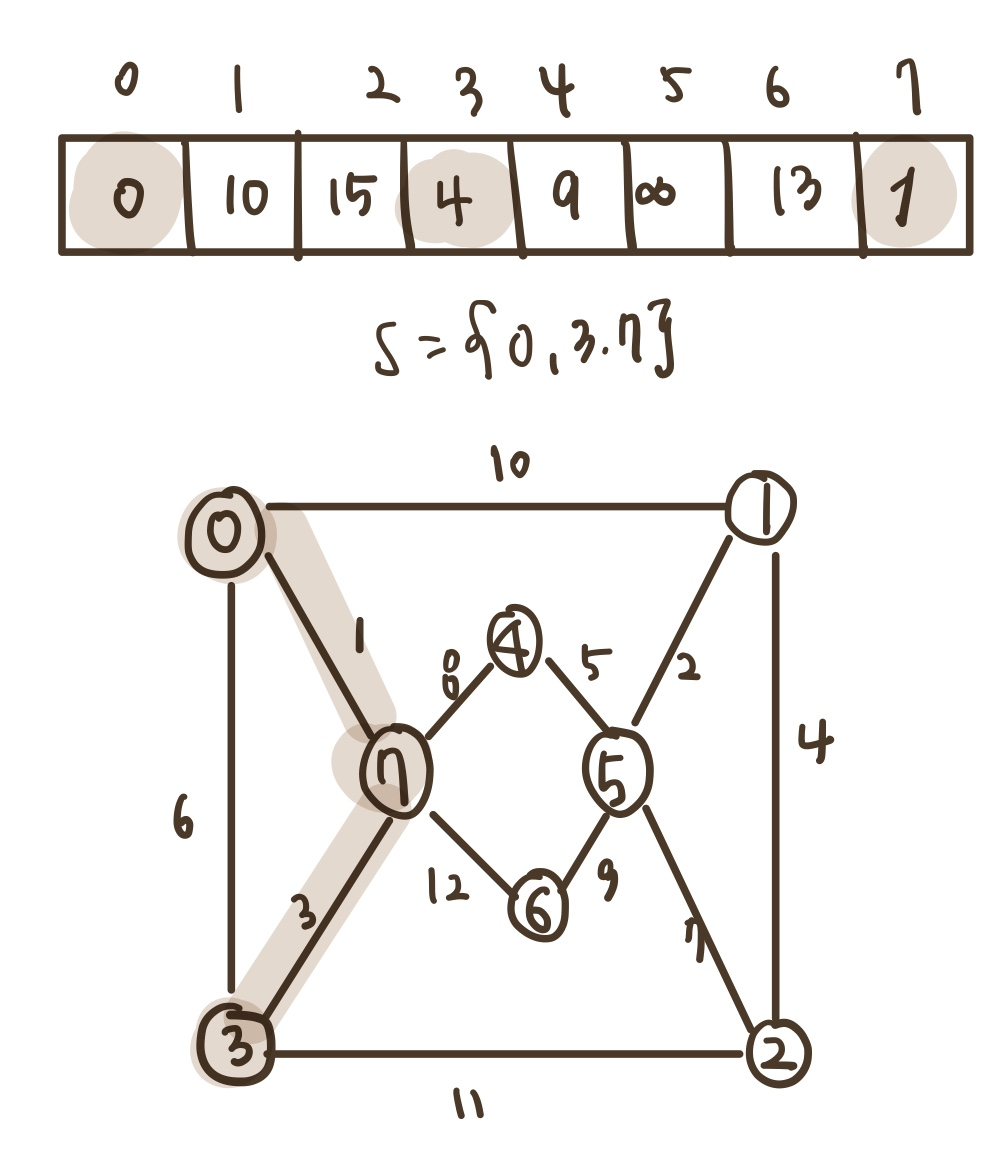
distance[0] = 0
distance[1] = min(distance[1], distance[3] + weight[3][1]) = min(10, ∞) = 10
distance[2] = min(distance[2], distance[3] + weight[3][2]) = min(∞, 15) = 15
distance[3] = 4
distance[4] = min(distance[4], distance[3] + weight[3][4]) = min(9, ∞) = 9
distance[5] = min(distance[5], distance[3] + weight[3][5]) = min(∞, ∞) = ∞
distance[6] = min(distance[6], distance[3] + weight[3][6]) = min(13, ∞) = 13
distance[7] = 1
4) 위의 과정을 반복한다.
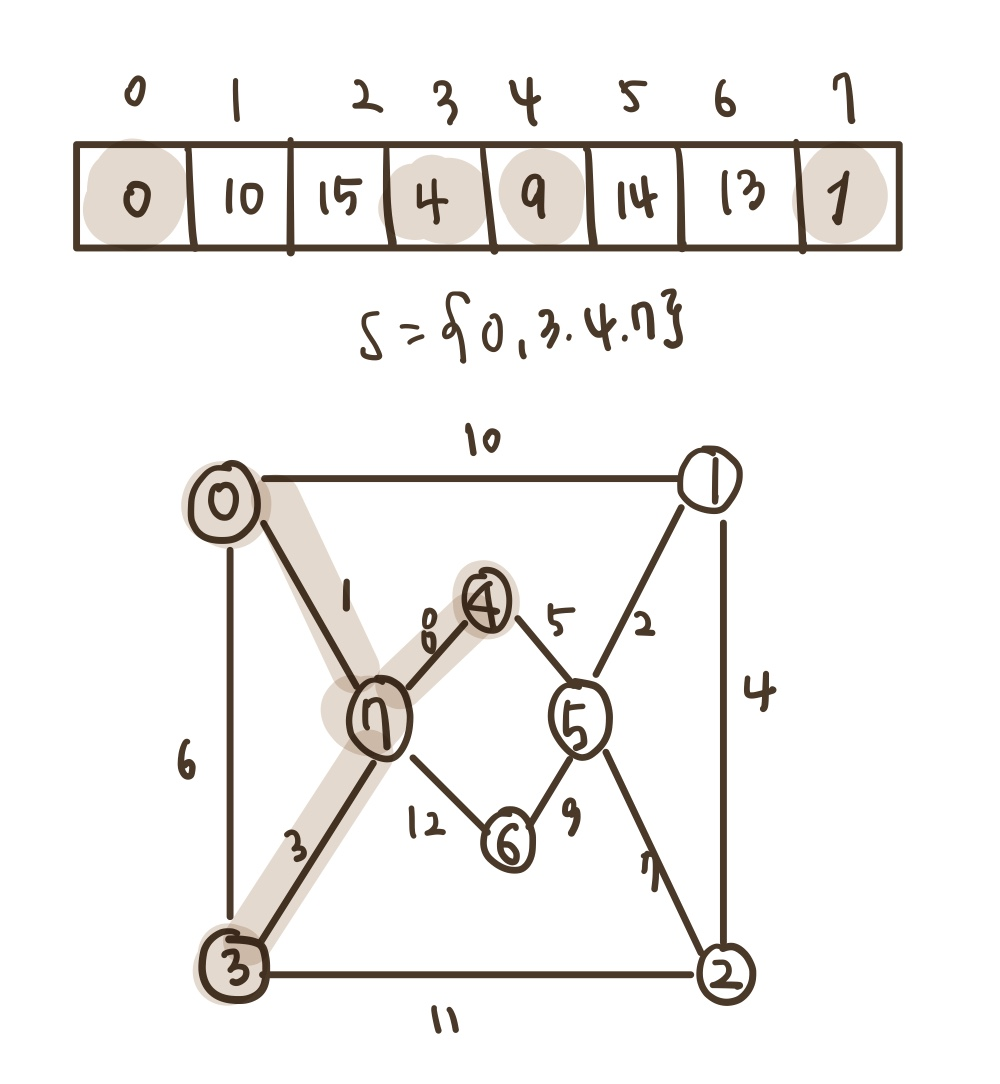
distance[0] = 0
distance[1] = min(distance[1], distance[4] + weight[4][1]) = min(10, ∞) = 10
distance[2] = min(distance[2], distance[4] + weight[4][2]) = min(15, ∞) = 15
distance[3] = 4
distance[4] = 9
distance[5] = min(distance[5], distance[4] + weight[4][5]) = min(∞, 14) = 14
distance[6] = min(distance[6], distance[4] + weight[4][6]) = min(13, ∞) = 13
distance[7] = 1
5)

distance[0] = 0
distance[1] = 10
distance[2] = min(distance[2], distance[1] + weight[1][2]) = min(15, 14) = 14
distance[3] = 4
distance[4] = 9
distance[5] = min(distance[5], distance[1] + weight[1][5]) = min(14, 12) = 12
distance[6] = min(distance[6], distance[1] + weight[1][6]) = min(13, ∞) = 13
distance[7] = 1
6)
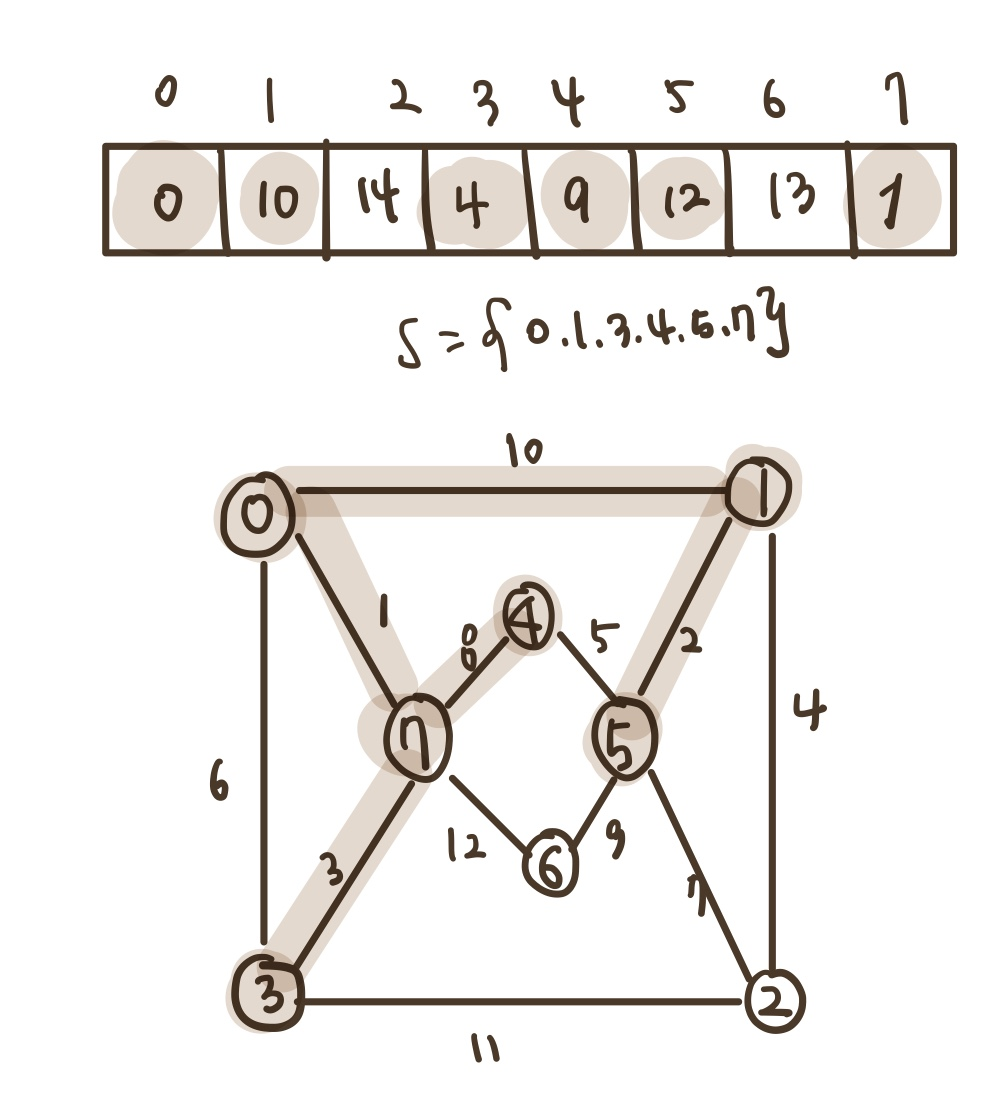
distance[0] = 0
distance[1] = 10
distance[2] = min(distance[2], distance[5] + weight[5][2]) = min(14, 19) = 14
distance[3] = 4
distance[4] = 9
distance[5] = 12
distance[6] = min(distance[6], distance[5] + weight[5][6]) = min(13, 22) = 13
distance[7] = 1
7)

distance[0] = 0
distance[1] = 10
distance[2] = min(distance[2], distance[6] + weight[6][2]) = min(14, ∞) = 14
distance[3] = 4
distance[4] = 9
distance[5] = 12
distance[6] = 13
distance[7] = 1
8)

distance[0] = 0
distance[1] = 10
distance[2] = 14
distance[3] = 4
distance[4] = 9
distance[5] = 12
distance[6] = 13
distance[7] = 1
/*
found[] : 방문한 정점 표시
distance[] : 시작정점으로부터의 최단경로
choose : distance가 가장 작은 distance[i]를 찾는 함수
*/
void shortest_path(GraphType *g, int start) {
int u, w;
for (int i=0; i<g->n; i++) { // 초기화
distance[i] = g->weight[start][i];
found[i] = FALSE;
}
found[start] = FALSE;
distance[start] = 0;
for (int i = 0; i<g->n-1; i++) {
u = choose(distance, g->n, found); // distance가 가장 작은 정점 u
found[u] = TRUE; // 방문 표시
for (w = 0; w<g->n; i++) {
if (!found[w])
if (distance[u] + g->weight[u][w] < distance[w])
distance[w] = distance[u] + g->weight[u][w];
}
}
}다익스트라 알고리즘은 n개의 정점이 있다면 n^2번 반복하므로 시간복잡도는 O(N^2)이다.
2. 플로이드 알고리즘
- 2차원 배열을 3중 반복하는 구조
- 인접 행렬 weight
아래의 두 가지 경우를 고려해야 한다.
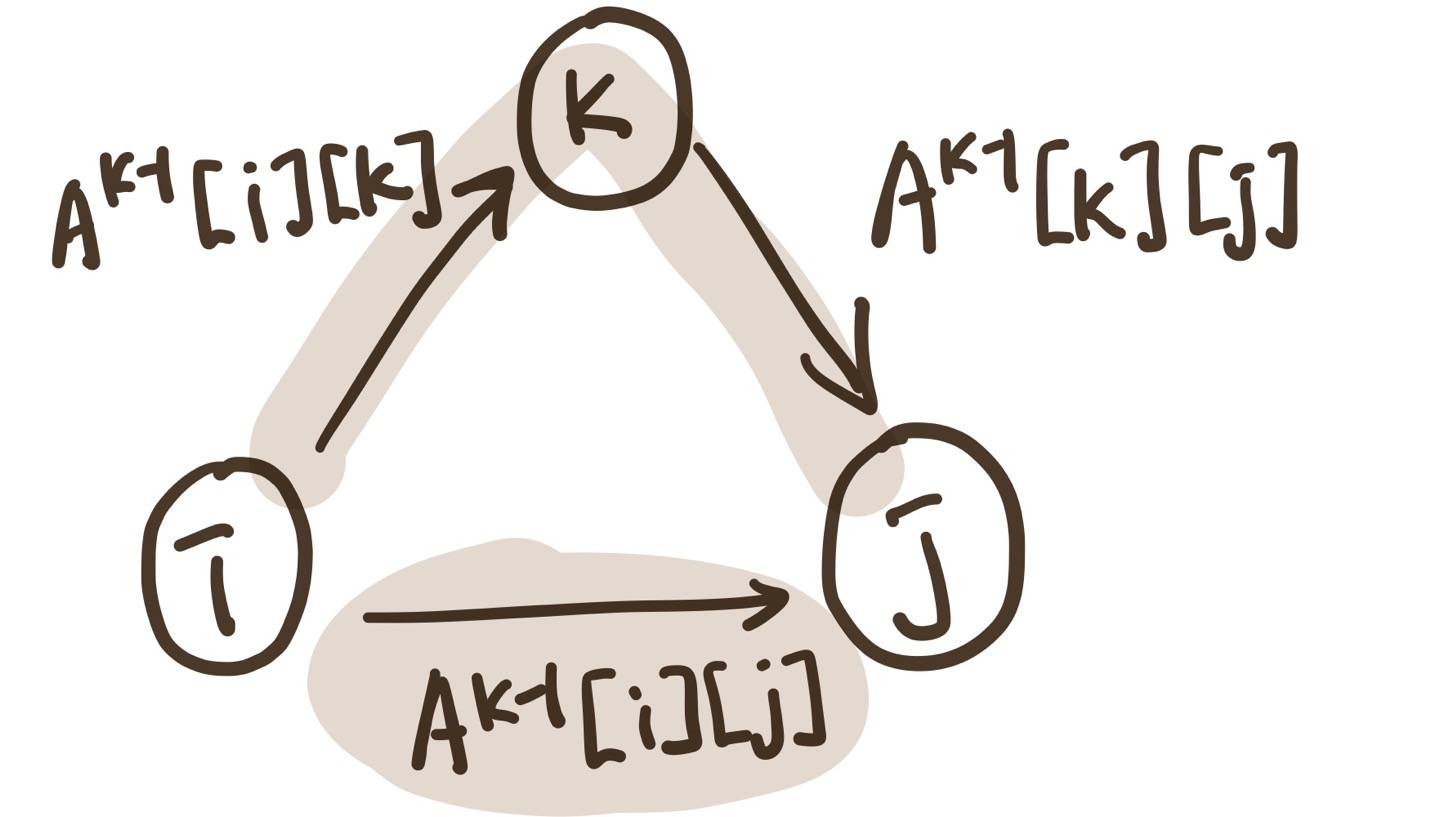
1) K를 거치는 경우
A[i][k] + A[k][j] 이 최단거리가 된다.
2) K를 거치지 않는 경우
A[i][j]이 최단거리가 된다
=> 1과 2 경우를 비교해 최단거리를 구한다.
1) 그래프의 가중치 행렬로 배열을 초기화 한다. 0~6을 거치는 경우를 파악한다.
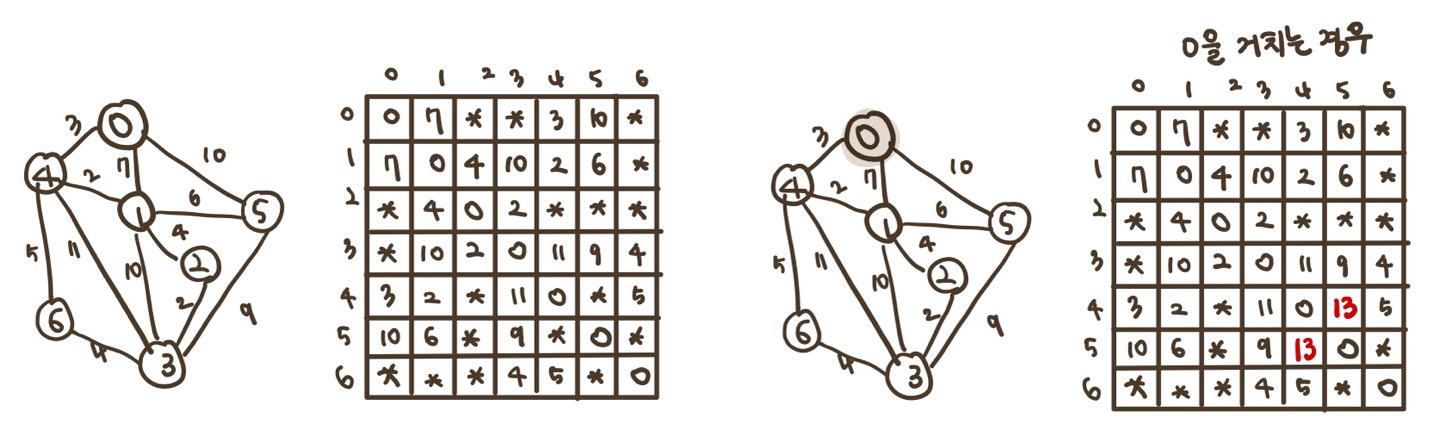
A[i][j] = min(A[i][j], A[i][0] + A[0][j]
2) 반복
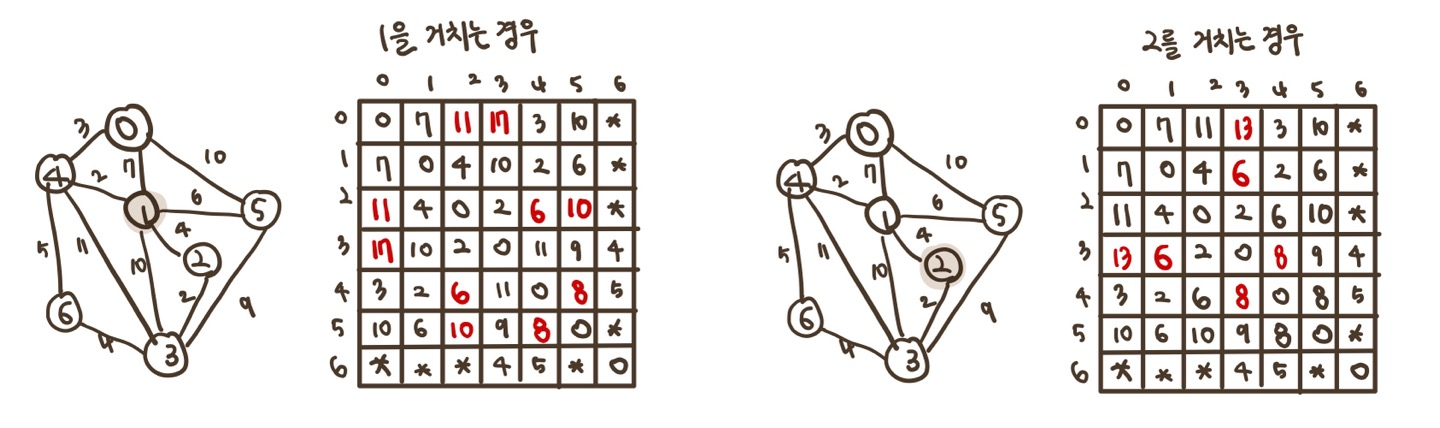
A[i][j] = min(A[i][j], A[i][1] + A[1][j]
A[i][j] = min(A[i][j], A[i][2] + A[2][j]
3)
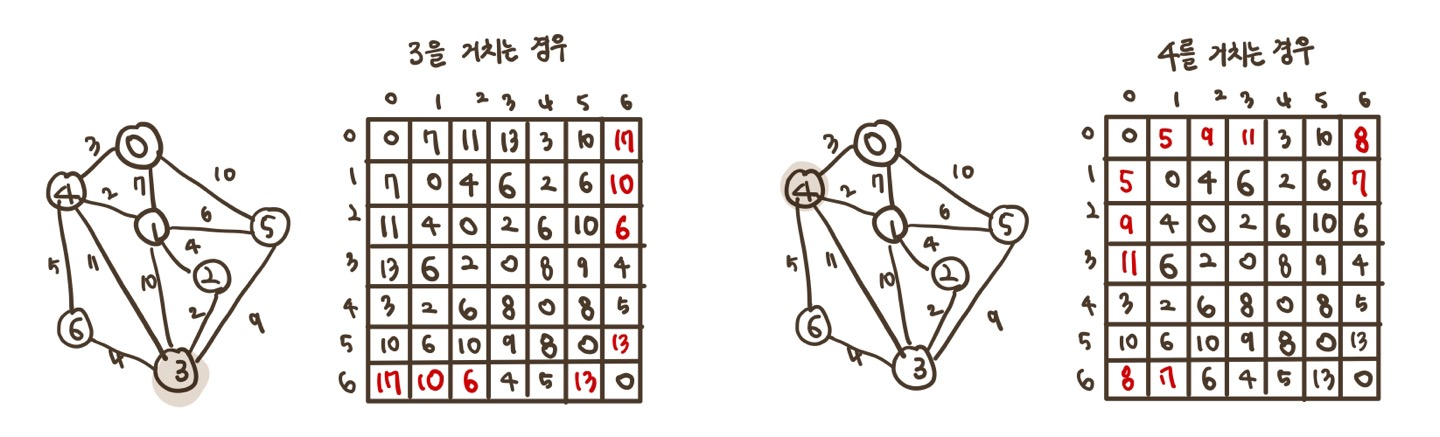
A[i][j] = min(A[i][j], A[i][3] + A[3][j]
A[i][j] = min(A[i][j], A[i][4] + A[4][j]
4)

A[i][j] = min(A[i][j], A[i][5] + A[5][j]
A[i][j] = min(A[i][j], A[i][6] + A[6][j]
void floyd(GraphType *g) {
for (int i = 0; i<g->n; i++) {
for (int j = 0; j<g->n; j++)
A[i][j] = g->weight[i][j];
}
for (int k = 0; k<g->n; k++) {
for (int i = 0; i<g->n; i++) {
for (int j = 0; j<g->n; j++) {
if (A[i][k] + A[k][j] < A[i][j])
A[i][j] = A[i][k] + A[k][j];
}
}
}
}
플로이드 알고리즘은 3중 반복 구조가 있기 때문에 시간복잡도는 O(N^3)이다.
728x90
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Tree(트리) - 레벨 순회 (0) | 2023.01.08 |
|---|---|
| [자료구조] Search(탐색) - 순차탐색과 이진탐색 (1) | 2023.01.08 |
| [자료구조] Graph(그래프) - 진출/진입 차수 계산 (0) | 2023.01.06 |
| [자료구조] Tree(트리) - 이진 트리의 순회 (0) | 2023.01.05 |
| [자료구조] Tree(트리) - 이진 트리 (0) | 2023.01.05 |
