728x90
트리를 순회하는 방법은 전위, 중위, 후위 순회가 있다.
레벨 순회는 표준적인 순회 방법은 아니지만 자주 사용된다.
레벨 순회(Level Order)
: 각 노드를 레벨 순으로 검사하는 순회 방법
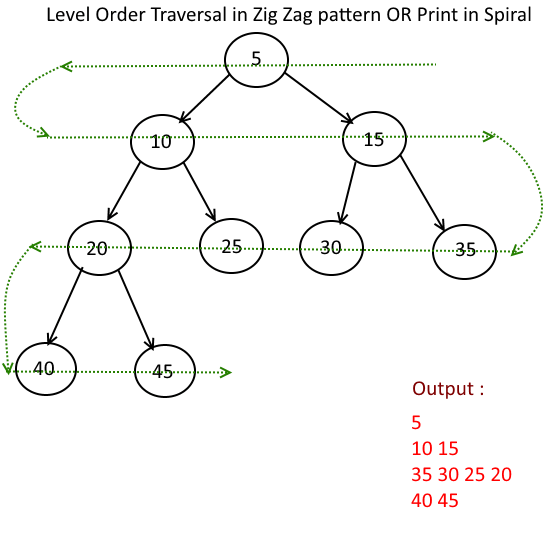
구현 원리는 다음과 같다.
1. ptr을 큐에 삽입한다.
2. 큐가 empty가 아닐 때 큐에서 삭제하고 삭제한 값을 ptr로 둔다.
3. ptr의 왼쪽 노드와 오른쪽 노드가 있다면 각각을 큐에 삽입한다.
4. 2~3 과정을 반복한다.
1) level_order(root)인 경우 초기 상태이다.

2) ptr이 5를 가리키므로 큐에 넣는다.
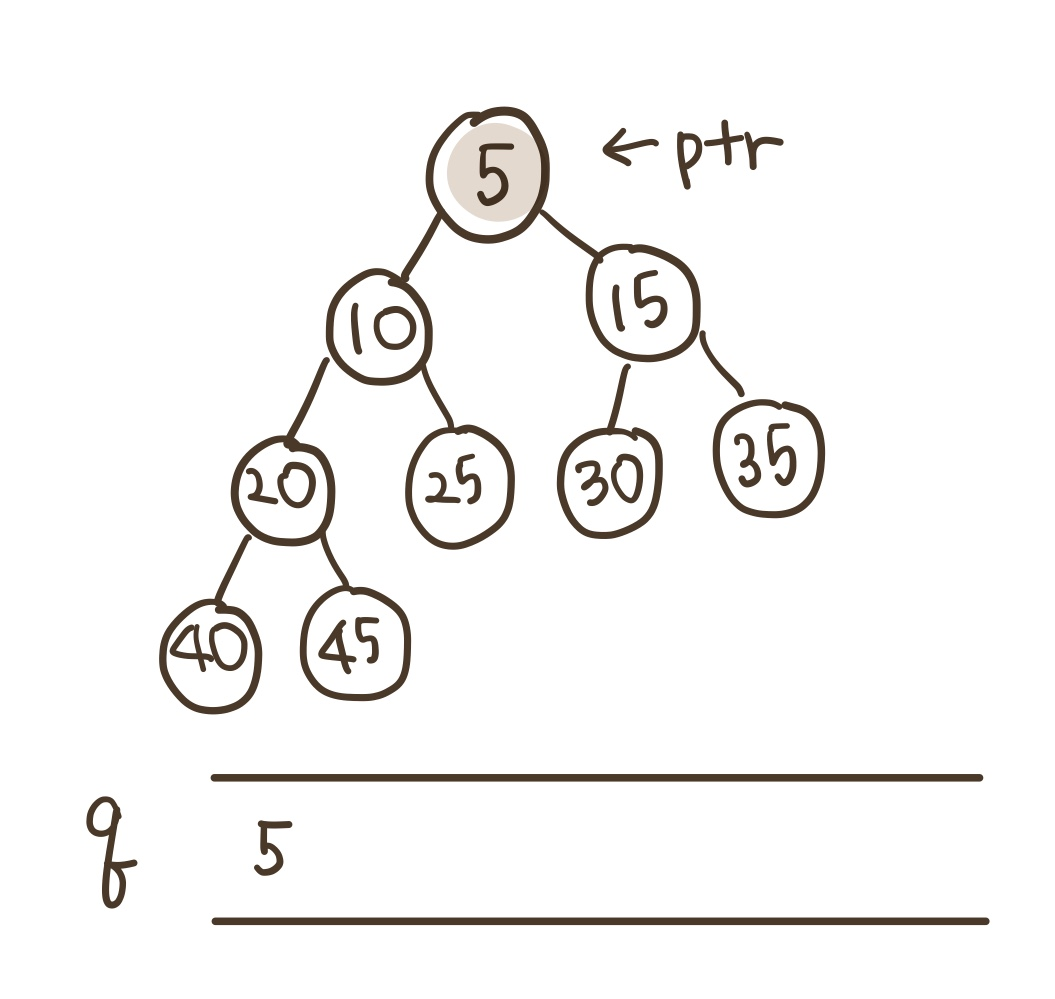
3) 5의 왼쪽과 오른쪽 자식이 존재하므로 차례대로 큐에 넣는다. ptr은 여전히 5를 가리킨다.
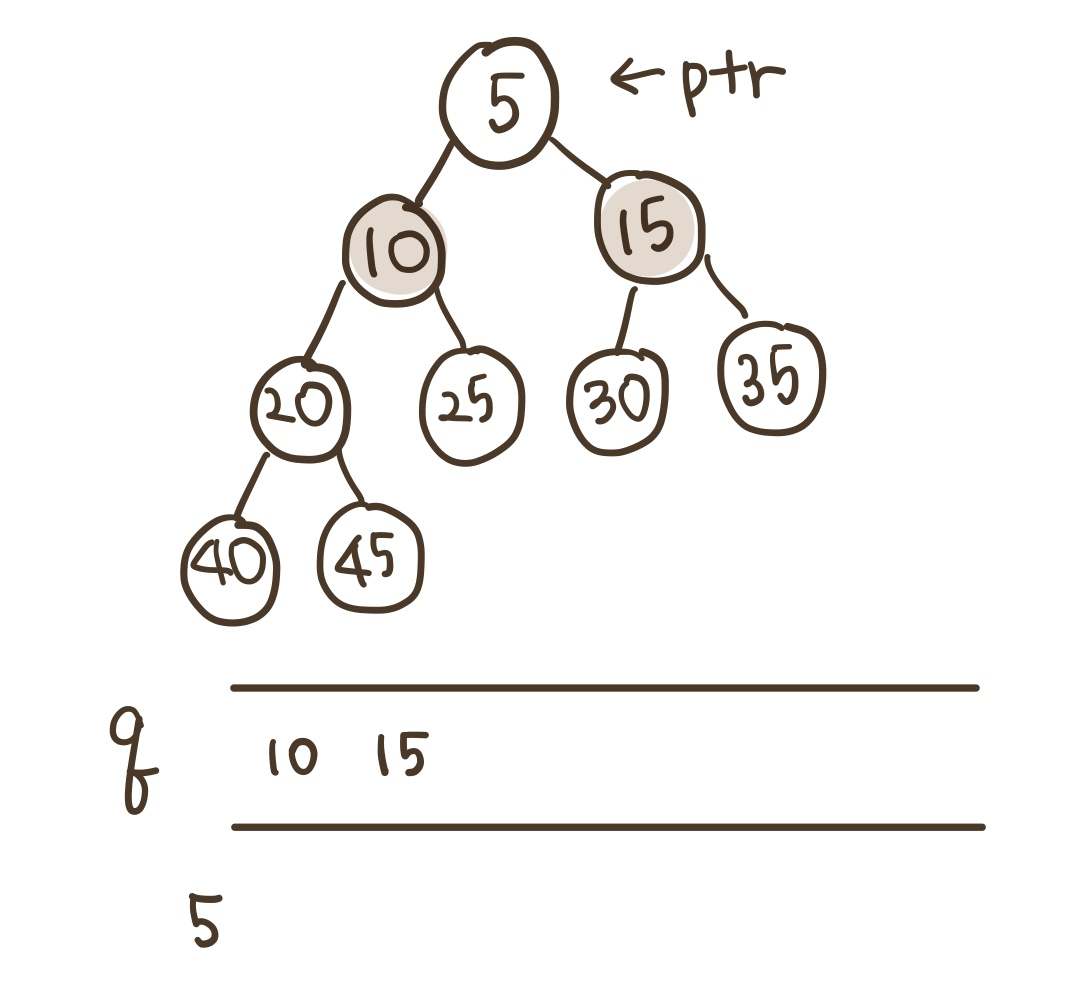
4) 큐에서 삭제한 값이 ptr이 되고 ptr의 왼쪽과 오른쪽 자식을 큐에 넣는다.

7) 큐에서 삭제한 값인 15를 ptr이 가리키고 15의 왼쪽과 오른쪽 자식을 차례대로 큐에 넣는다.

8) 큐에서 삭제한 값인 20이 ptr이 되고 20의 왼쪽과 오른쪽 자식을 차례로 큐에 넣는다.
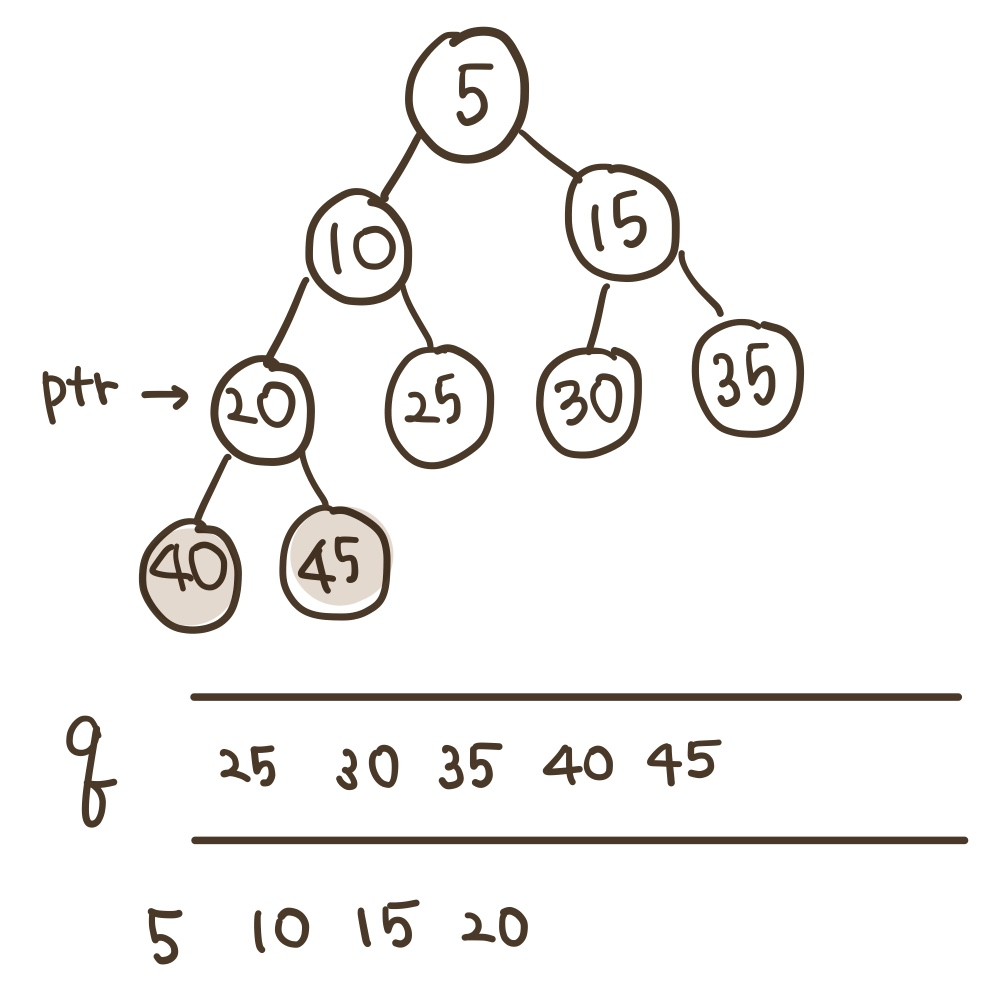
9) 큐에서 삭제한 값인 25가 ptr이 되고 25는 왼쪽과 오른쪽 자식 모두 없으므로 큐의 변화는 없다.
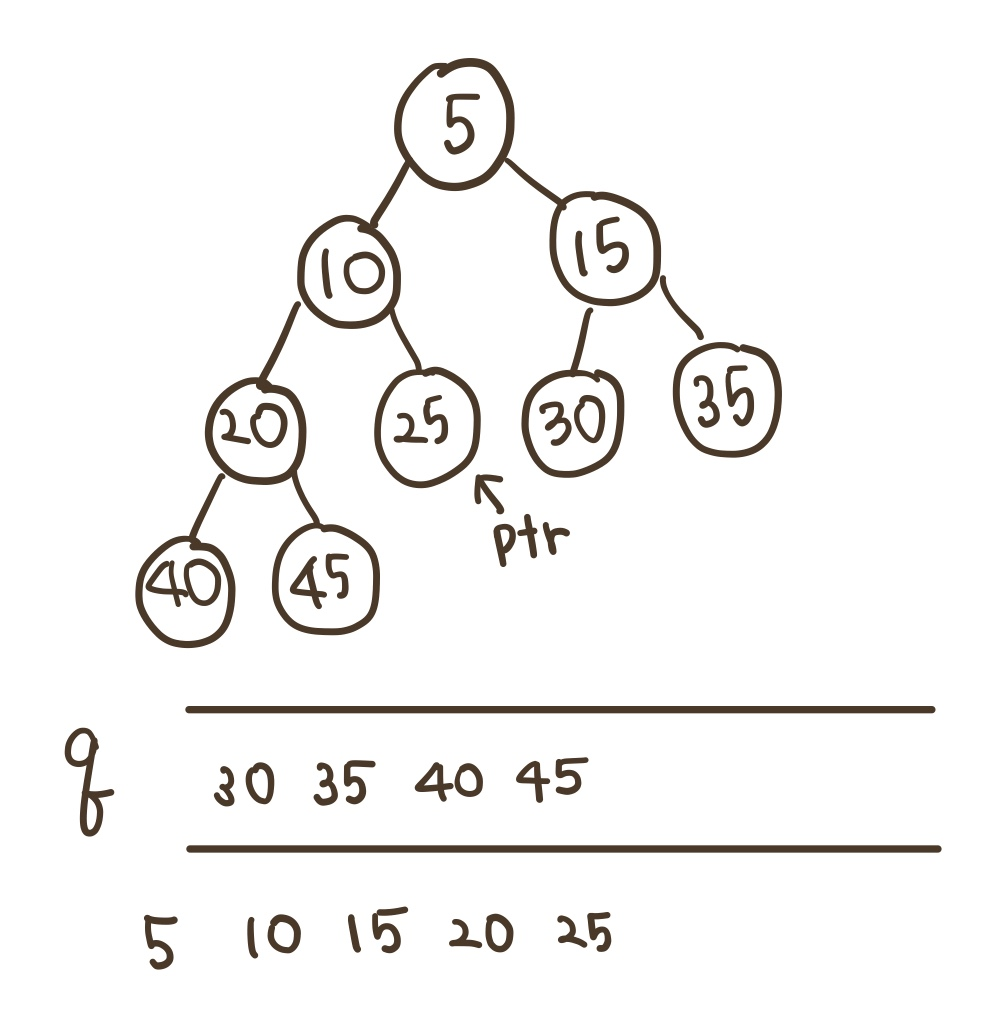
10) 나머지 모두 리프 노드이므로 9를 반복한다.

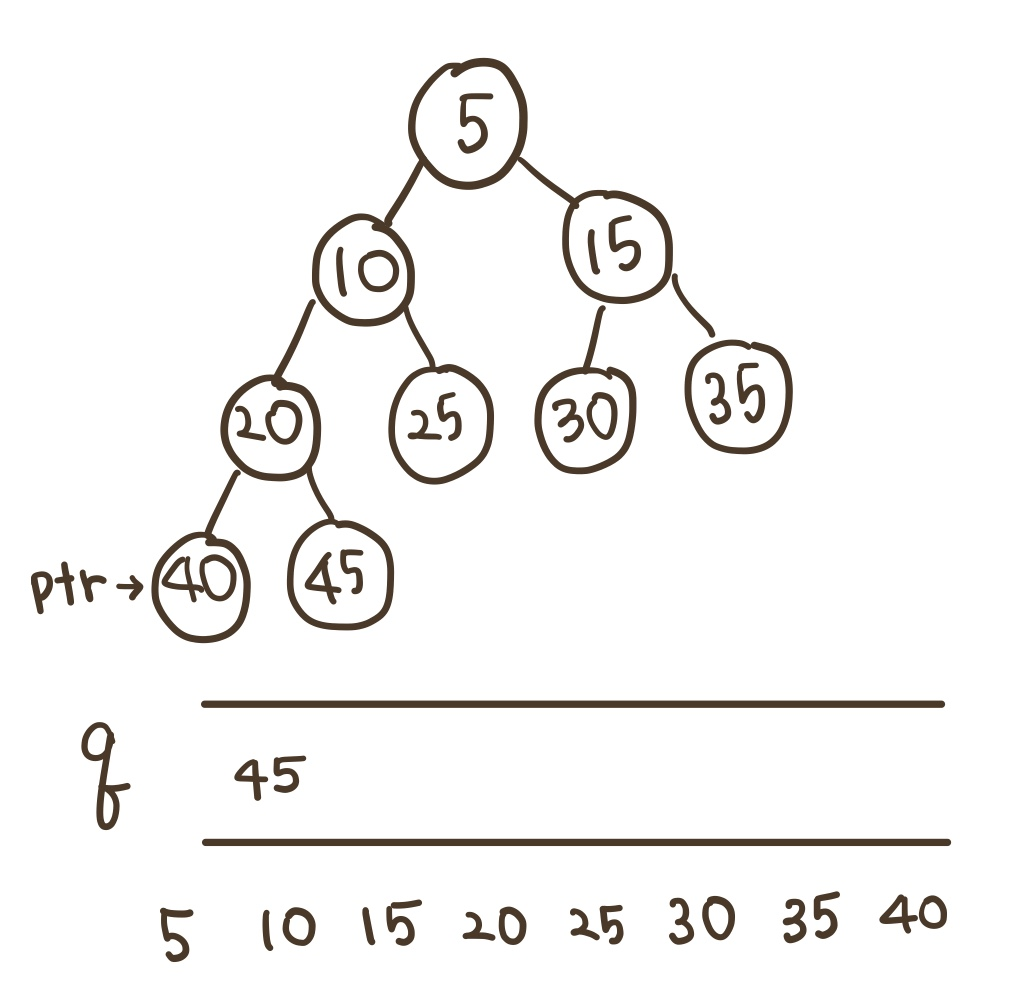
11)

12)
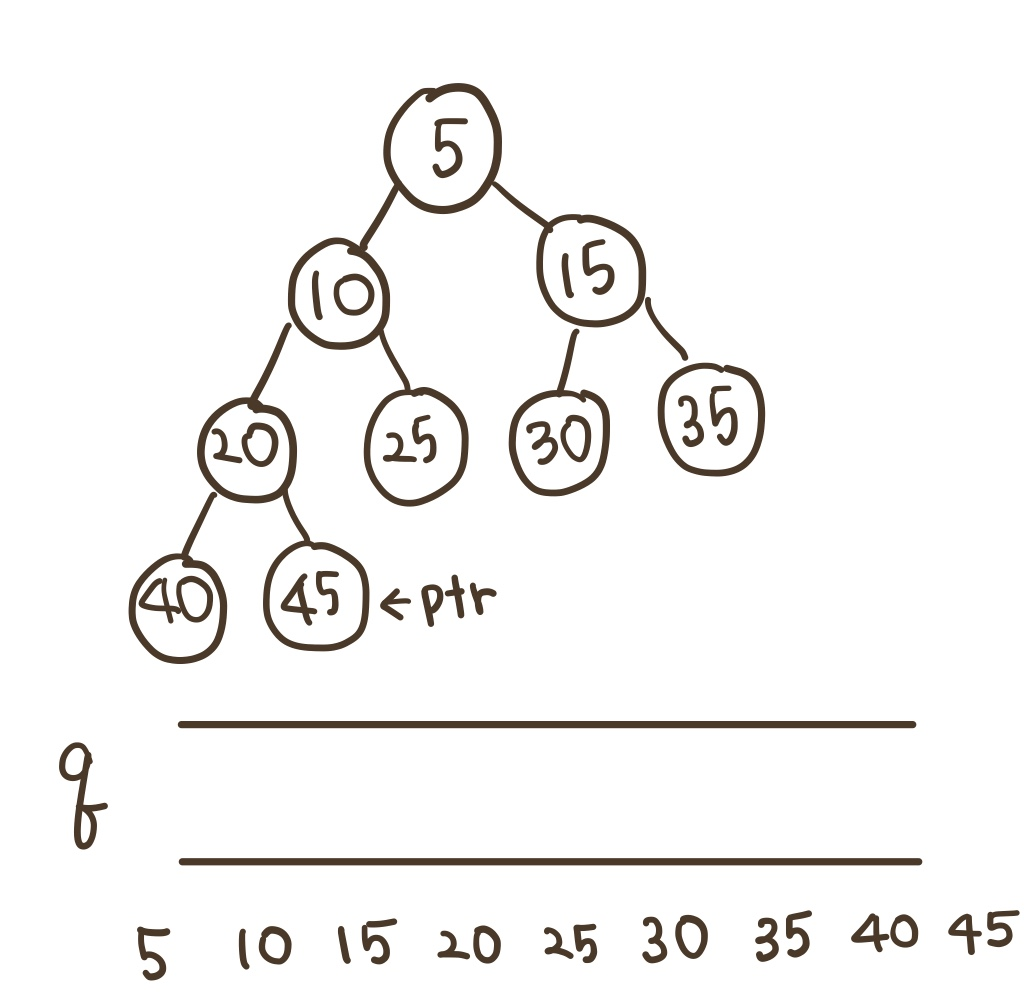
13) 큐가 empty이므로 중단한다.
실행 코드는 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
typedef struct TreeNode {
int data;
struct TreeNode *left, *right;
} TreeNode;
#define MAX_QUEUE_SIZE 100
typedef TreeNode * element;
typedef struct { // 큐 타입
element data[MAX_QUEUE_SIZE];
int front, rear;
} QueueType;
void error(char *message) {
fprintf(stderr, "%s\n", message);
exit(1);
}
void init_queue(QueueType *q) {
q->front = q->rear = 0;
}
int is_empty(QueueType *q) {
return (q->front == q->rear);
}
int is_full(QueueType *q) {
return ((q->rear + 1) % MAX_QUEUE_SIZE == q->front);
}
void enqueue(QueueType *q, element item) {
if (is_full(q))
error("Full");
q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
q->data[q->rear] = item;
}
element dequeue(QueueType *q) {
if (is_empty(q))
error("Empty");
q->front = (q->front + 1) % MAX_QUEUE_SIZE;
return q->data[q->front];
}
void level_order(TreeNode *ptr) {
QueueType q;
init_queue(&q);
if (ptr == NULL) return;
enqueue(&q, ptr);
while (!is_empty(&q)) {
ptr = dequeue(&q);
printf("%d", ptr->data);
if (ptr->left)
enqueue(&q, ptr->left);
if (ptr->right)
enqueue(&q, ptr->right);
}
}
TreeNode n1 = { 1, NULL, NULL };
TreeNode n2 = { 4, &n1, NULL };
TreeNode n3 = { 16, NULL, NULL };
TreeNode n4 = { 25, NULL, NULL };
TreeNode n5 = { 20, &n3, &n4 };
TreeNode n6 = { 15, &n2, &n5 };
TreeNode *root = &n6;
int main(void)
{
level_order(root);
return 0;
}
참고
c언어로 쉽게 풀어쓴 자료구조
728x90
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Tree(트리) - 스레드 이진 트리 (0) | 2023.01.14 |
|---|---|
| [자료구조] Tree(트리) - 수식 트리 (0) | 2023.01.08 |
| [자료구조] Search(탐색) - 순차탐색과 이진탐색 (1) | 2023.01.08 |
| [자료구조] Graph(그래프) - 최단 경로 알고리즘 (0) | 2023.01.07 |
| [자료구조] Graph(그래프) - 진출/진입 차수 계산 (0) | 2023.01.06 |
