Reinforcement Learning
강화학습에 대해서 이해하기 위해서 아래 두 가지 문제를 예시로 알아볼 것이다. 먼저, 이 두 문제에 대한 기본적인 정의를 알아보자.
다중 손잡이 밴딧 문제
$1을 넣고 여러 손잡이 중에 하나를 골라서 당기면 $1을 잃거나 따는 문제이다. 손잡이마다 승률은 정해져 있는데 사용자는 확률을 모른다는 전제가 깔려 있다. 행동 - 상태 변화 - 보상의 학습 사이클에서 상태가 없는 단순한 문제이다.
- 탐험형 정책(exploration policy) : 처음부터 끝까지 무작위로 선택
- 탐사형 정책(exploitation policy) : 몇 번 시도해보고 승률이 높은 손잡이만 당기는 것
강화학습에서는 게임을 시작해서 끝날 때까지 기록을 에피소드라고 하며, 에피소드가 길면 확률을 통해서 최적 정책을 알아낼 수 있다. 이때, 위의 두 가지 정책의 적절한 조화가 필요한데, 탐욕 알고리즘을 변형한 ε-탐욕 알고리즘을 적용할 수 있다. 아니면 여러 번 시행한 결과를 바탕으로 학습시키는 방법도 있다.
FrozenLake 문제
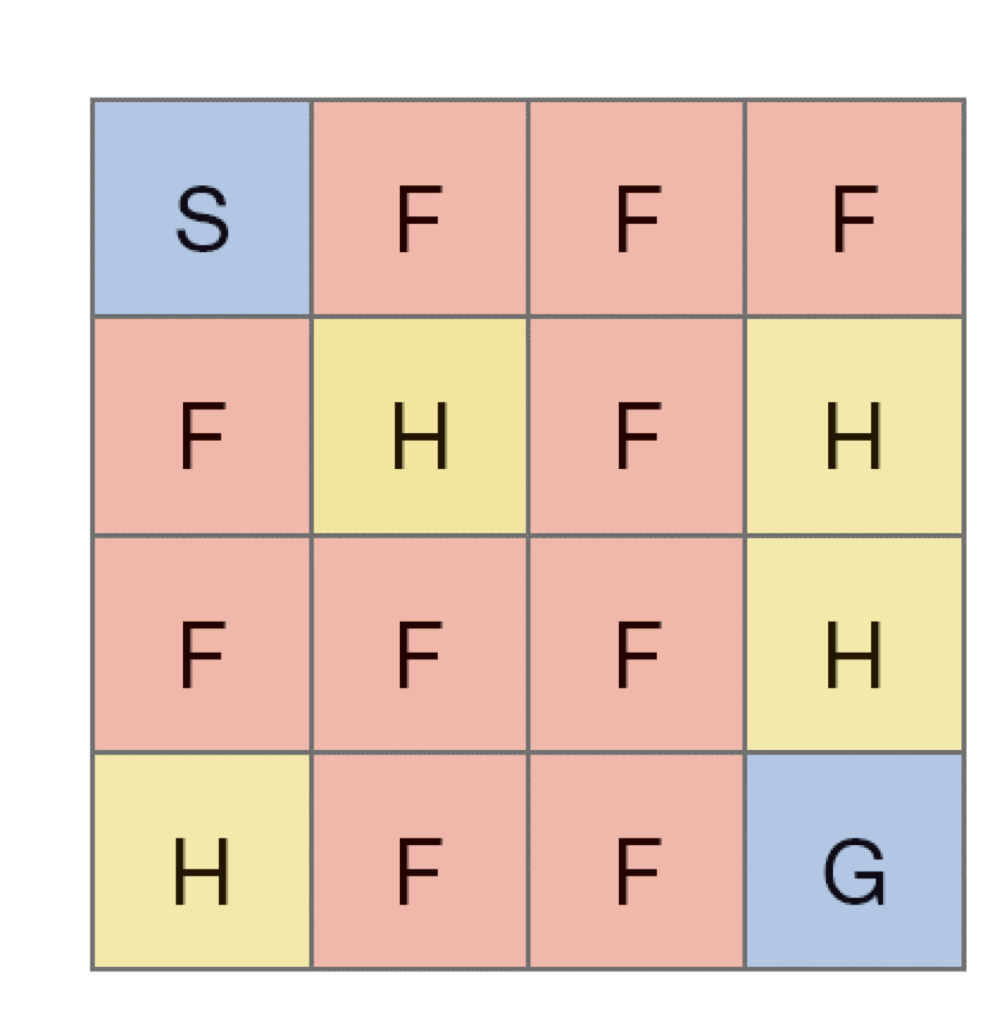
OpenAI의 gym 라이브러리를 사용하면 FrozenLake 문제를 접할 수 있다. 이때, 아래 그림처럼 S에서 출발해서 G에 도착하면 이기는 게임이다. F는 얼어 있어서 밟고 지나갈 수는 있지만, H은 구멍이라 빠지면 지는 규칙이다. 현재 있는 곳이 state, 좌우상하의 이동을 action으로 본다.
계산 모형
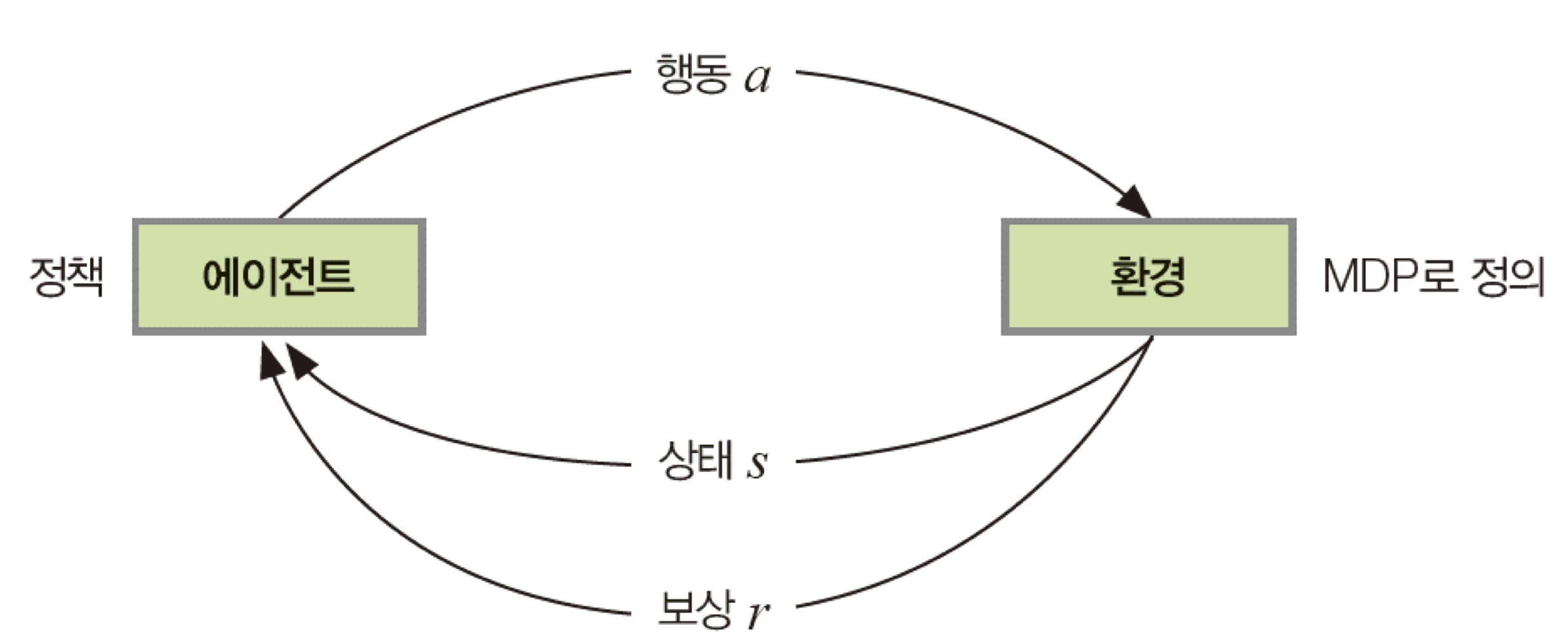
위의 문제들에 공통적으로 사용한 것이 마르코프 결정 프로세스(MDP)이다. 상태의 종류와 행동의 종류, 보상의 종류를 지정하고 행동했을 때 발생하는 상태 변환을 지배하는 규칙을 정의한다. 그래서 상태집합 S, 행동집합 A, 보상집합 R을 정의할 수 있다.
- 다중 손잡이 밴딧
- 상태집합 S=∅
- 행동집합 A={손잡이0, 손잡이1, 손잡이2, 손잡이3, 손잡이4}
- 보상집합 R={1, -1}
- FrozenLake
- 상태집합 S={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}
- 행동집합 A={0, 1, 2, 3}
- 보상집합 R={0,1}
참고로 다중 손잡이 밴딧 문제 같은 경우에 보상이 즉시 이루어지지만, FrozenLake나 앞으로 배울 바둑, 장기, 비디오 게임 등은 결과에 도달해야만 보상을 얻을 수 있다. 상태 전이에서도 2가지 환경으로 나눌 수 있다. 100% 확률로 새로운 상태가 정해지는 확률인 결정론적 환경과 확률 분포에 따라서 새로운 상태가 다르게 정해지는 환경인 스토캐스틱 환경이다. 우리는 결정론적 환경인 경우에만 고려할 것이다.
지도학습과 차이
강화학습과 지도학습은 여러 측면에서 다르다. 앞으로 설명할 것이지만, 간단하게 요약하자면 아래와 같다.
| 지도학습(신경망) | 강화학습 | |
| 문제(데이터) | 훈련집합 x(특징 벡터)와 y(레이블) | 환경이나 환경에서 수집한 데이터 |
| 최적화 목표 | 신경망 출력 o와 레이블 y의 오차 최소화 | 누적 보상 최대화 |
| 학습 알고리즘이 알아내야 하는 것 | 오차를 최소화하는 신경망의 가중치 | 누적 보상을 최대화하는 최적 정책 |
| 품질 평가 함수 | 손실 함수 | 가치 함수 |
| 학습 알고리즘 | 스토케스틱 그레이디언트 하강법(SGD) | 동적 프로그래밍, SARSA, Q-Learning, DQN 등 |
최적 정책
학습 알고리즘이 해야하는 일은 누적 보상을 최대화하는 최적 정책을 알아내는 것이다. 예를 들어서, 다중 손잡이 밴딧 문제에서 승률이 가장 높은 손잡이를 당기는 정책과 같다. 또 FrozenLake 문제에서 G에 도달할 수 있는 가장 안정적인 길을 택하는 것과 같다. Policy는 확률 분포로 표현할 수 있는데, P(a=i|s=j) 는 상태 변수 s가 j라는 값일 때 행동 변수 a가 i라는 값을 취할 확률을 말한다.
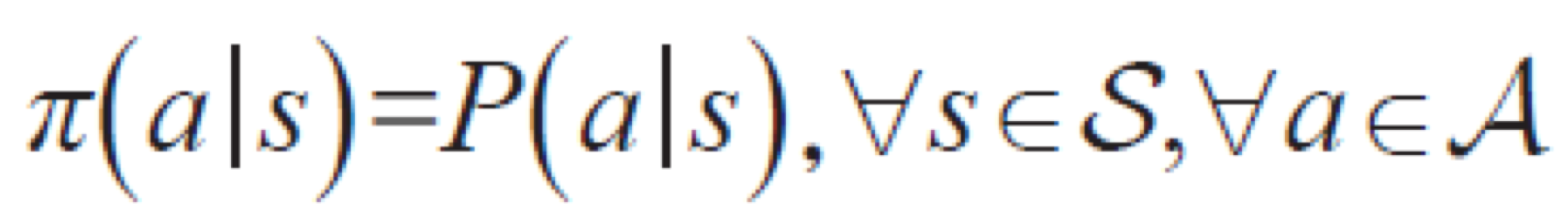
이렇게 누적 보상을 최대화하는 최적 정책을 알아내려면, 최적 정책이 정말 '최적'인지 판단해야 한다. 그래서 정책의 품질을 평가하는 함수인 가치 함수가 필요하다. 가치 함수는 가능한 모든 값을 검사해서 누적 보상이 최대인 것을 찾는다. 가치 함수는 아래와 같은 수식으로 계산할 수 있다.

예를 들어서, FrozenLake 문제에서 Down을 1, Right를 2로 정의하고 각 확률이 0.5로 선택하는 정책을 π1이라고 하자. 그러면 위의 공식을 사용해서 s=10일 때 가치함수를 계산해보자. P(z1)r(z1) + P(z2)r(z2)이므로 0.5*0 + 0.5*1.0*1 = 0.5로 계산할 수 있다.
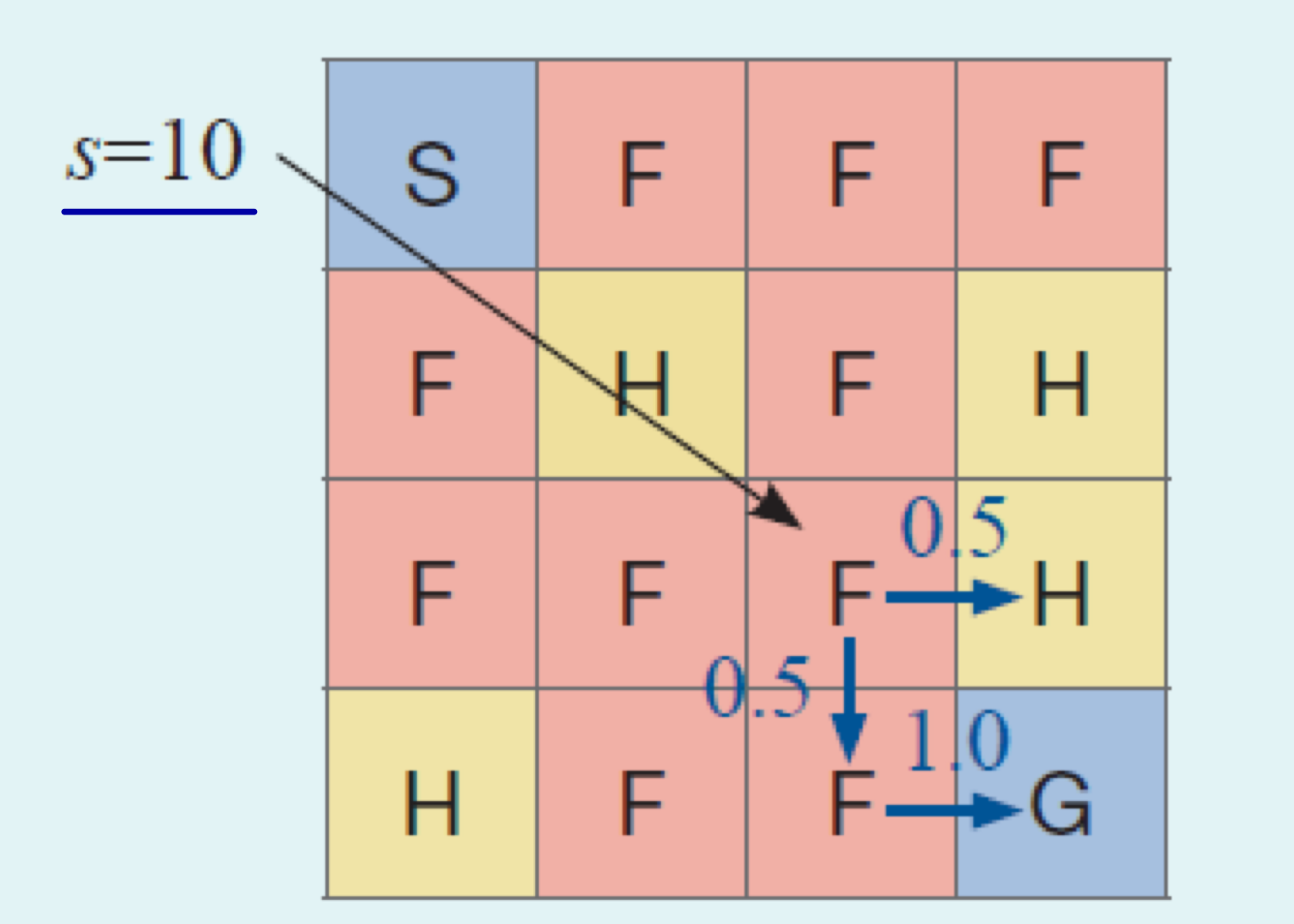
이 문제에서는 쉽게 계산할 수 있지만 1000*1000 같이 큰 격자를 가진 문제에 적용하면 계산이 복잡해진다. 그래서, 상태가 서로 밀접한 관련성을 가진다는 특징을 활용한 벨만 기대 방정식(Bellman Expectation Equation)이 있다. 다음 state에 대한 가치함수와 보상을 더한 값을 확률과 곱하여 계산한다.
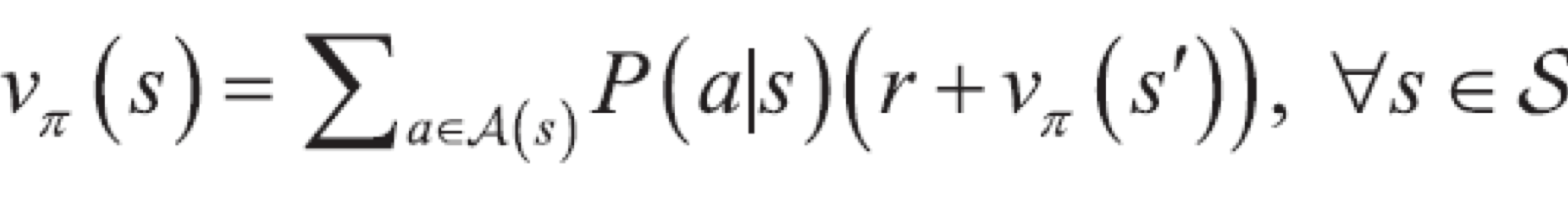
위의 가치 함수와 벨만 기대 방정식을 비교해보자. s=6일 때를 계산하면, P(z1)r(z1) + P(z2)r(z2) + P(z3)r(z3)이므로, 0.5*0 + 0.5*0.5*0 + 0.5*0.5*1.0*1 = 0.25이다. 벨만 기대 방정식을 계산하면 P(2|6)(0+v(7)) + P(1|6)(0+v(10) = 0.25이다.
실제로는 미래에 발생하는 보상의 가치를 일정 비율로 삭감하는 할인율을 포함한 벨만 기대 방정식을 사용한다. 누적 보상액 r(z)는 현재 순간에서 시작해 에피소드가 끝날 때까지 발생한 보상의 총합이기 때문이다.
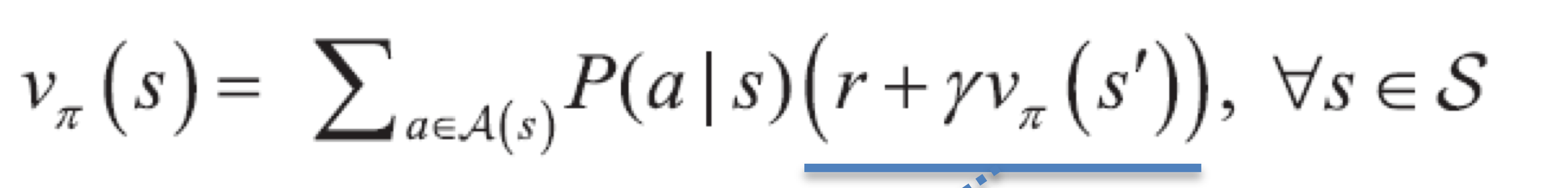
그래서 위에서 설명한 가치 함수는 상태 가치 함수라고 한다. 상태와 행동에 대한 함수인 행동 가치 함수도 있다.
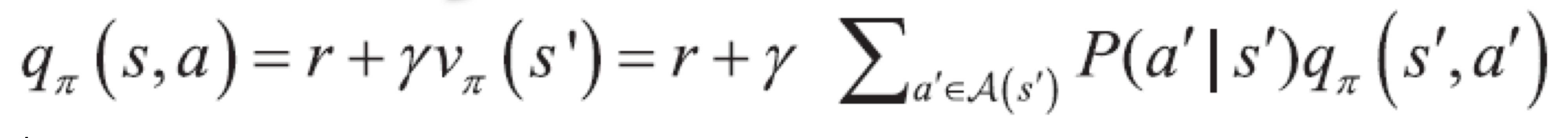
동적 프로그래밍
동적 프로그래밍을 통해서 최적의 정책을 알아낼 수도 있다.
정책 반복 알고리즘
가치 함수를 계산해서 반복하는 알고리즘인데, 가치 함수 계산에 너무 오랜 시간이 소요되고 계산이 복잡해 잘 사용하지 않는다.
가치 반복 알고리즘
벨만 최적 방정식을 사용해서 가치 함수를 계산한다.

동적 프로그래밍은 부트 스트랩 방식이라서 모든 상태가 부정확한 값으로 시작해 이웃 상태와 정보를 주고 받으면서 점차 수렴해가는 방식이다. 그래서 마르코프 결정 프로세스를 알아야만 적용가능 하고 크기가 작은 문제에만 적용할 수 있기 때문에 적용하는데 한계가 있다.
학습 기반 알고리즘
이러한 한계점이 있는 동적 프로그래밍 대신, 훈련 데이터를 활용하여 학습을 기반으로 한 알고리즘이 있다. 상태 전이 확률이 없는 경우에도 사용할 수 있고 환경을 시뮬레이션하여 데이터를 수집한다.
몬테카를로 방법
먼저, 에피소드에서 데이터를 수집한다, 상태를 중심으로 에피소드를 잘라 데이터를 수집하는 방식이다.
시간차 학습 알고리즘
기존의 몬테카를로 방식에서는 모든 샘플이 종료 순간까지 도달해야 한다. 종료 순간까지 가야 누적 보상액을 알 수 있기 때문이다. 그래서 종료 순간까지 가지 않고도 이웃 상태로 전환해 가치 함수를 개선하는 방식에 대해 고민한 끝에 아래 두가지 방식이 나왔다.
먼저, Sarsa 방식은 s-a-r-s'-a'의 고리를 만들어서 식에 대입해 가치 함수를 개선한다. 행동 a'을 결정할 마땅한 방법이 없어서 현재 가치 함수 q에 의존하고 있다. 이를 켜진 정책 방식이라고 한다. 이때 개선된 q가 아니라 기존 q를 기반으로 다음 행동이 정해진다.
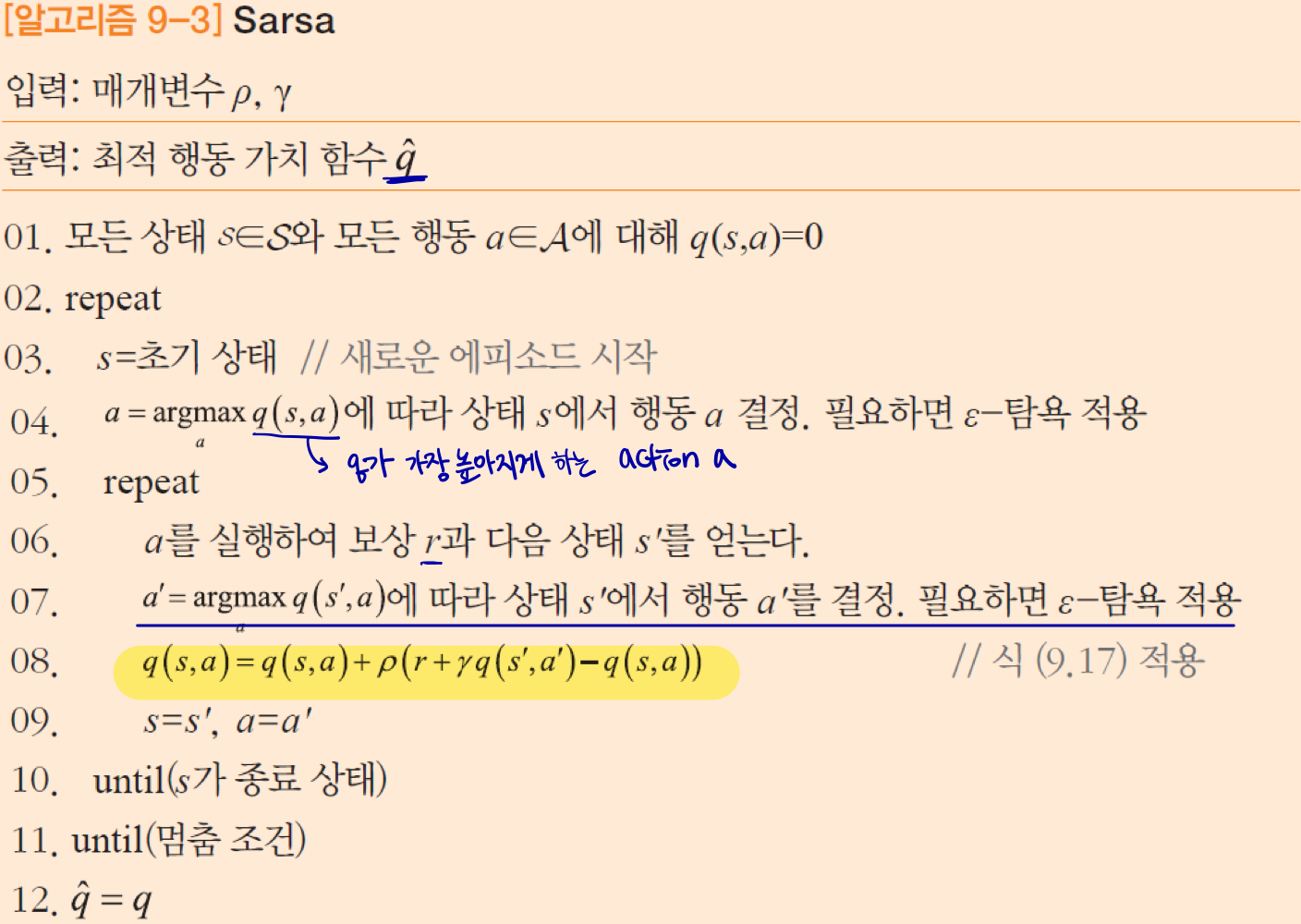
다음으로 Q Learning은 가치 함수 q에 의존하는 대신에 max 연산자를 사용한다. 모든 데이터가 존재하지 않아도 가치 함수를 구할 수 있고, 개선된 q를 기반으로 다음 행동이 결정된다는 점에서 Sarsa와 다르다. 이를 꺼진 정책 방식이라고 한다.

상태 가치 함수를 표현하는 v나 행동 가치 함수를 표현하는 q는 각각 1차원, 2차원 배열에 저장되는데 이를 참조표 방식이라고 한다. 동적 프로그래밍과 마찬가지로, 테이블을 사용하기 때문에 바둑처럼 상태의 개수가 방대한 경우 참조표 방식은 비현실적이라는 한계가 존재한다.
Deep Q Network
그렇다면, 참조표 없이 가치 함수를 계산할 수는 없을까? 바로 신경망을 사용하면 가치 함수를 표현할 수 있다. 이때 가장 중요한 문제는 학습에 사용할 훈련 집합을 수집하는 방법을 찾는 것이다. DQN은 딥러닝과 Q 러닝을 결합해 뛰어난 성능을 달성하는 신경망 모델이다.
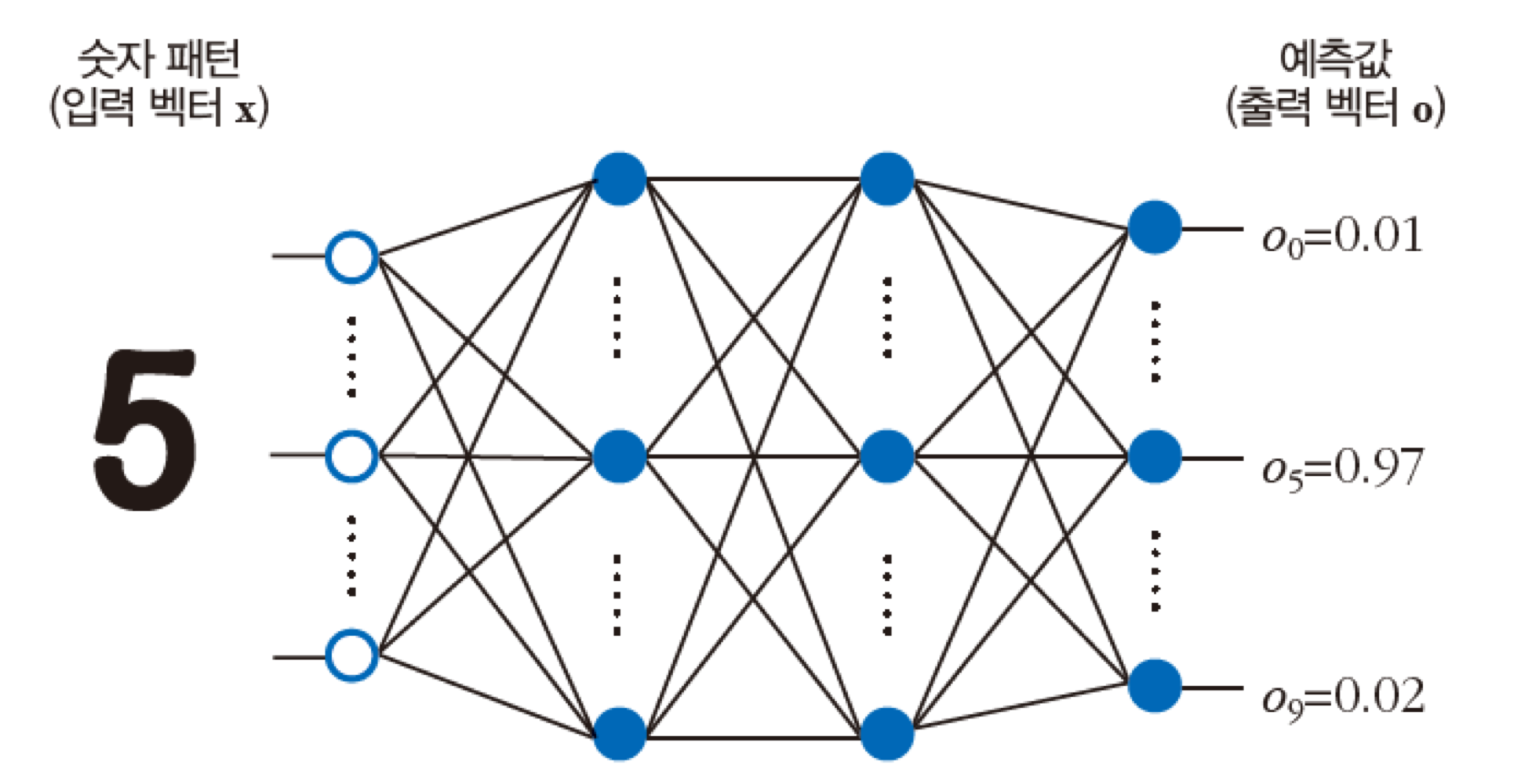
그렇다면 이러한 신경망을 어떻게 만들 수 있을까? 바로 Deep Neural Network를 사용하면 최적 정책 π를 추론할 수 있다. Q 러닝에서 생성되는 에피소드로부터 샘플들을 훈련 집합에 사용한다.
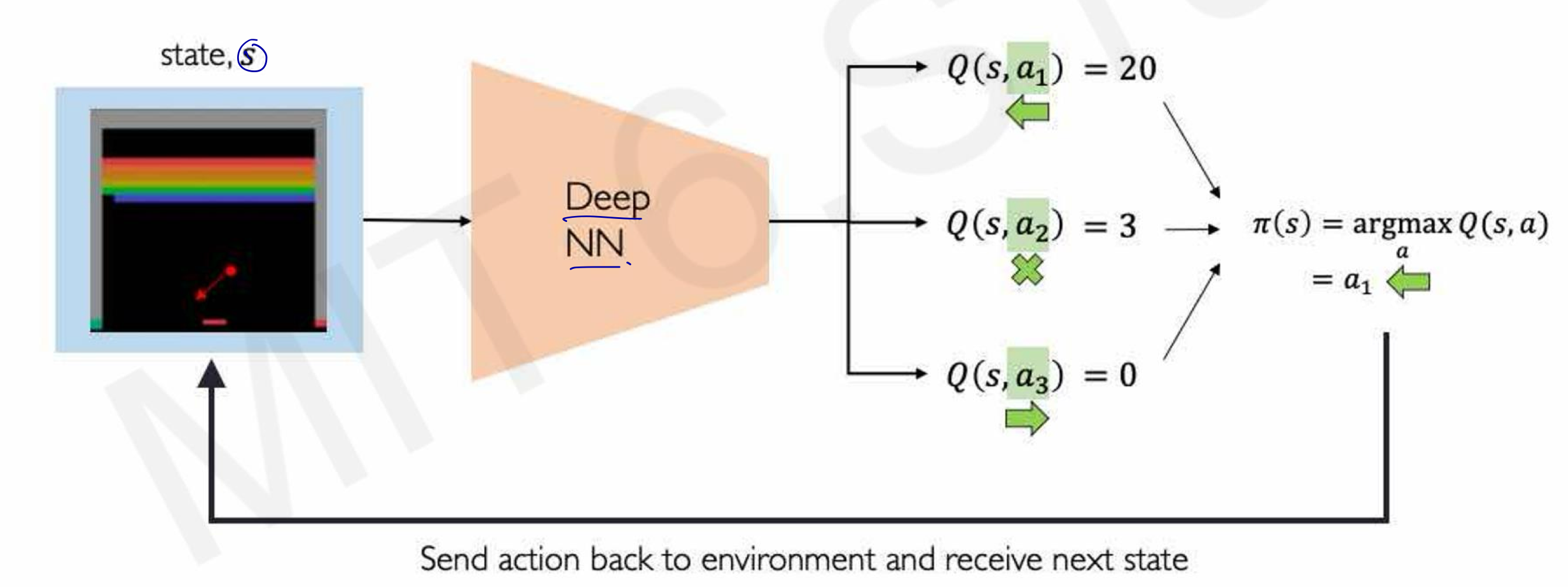
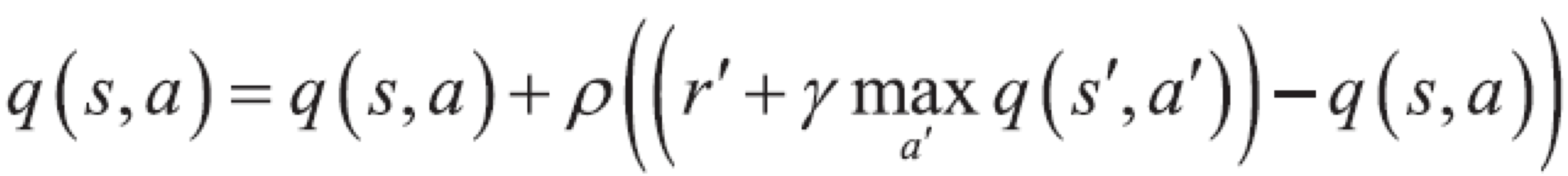
이러한 강화 학습은 강한 인공지능과 유사하다. 비지도 학습, 자율 플레이로 학습이라는 점이 유사하다. 예시로 자율주행 연구에 사용할 수 있다. 자동차가 올바른 경로로 가면 보상을 주고 행동하도록 한다. 그러나 사고가 발생하지 않는 쪽으로 학습하려면 사고가 발생해야 개선할 수 있다는 점, 사고가 발생한 샘플 데이터를 수집해야 한다는 점이 아직까지 한계로 남아있다. 알파고 같은 경우에도 바둑 기사들의 수를 지도 학습으로 훈련한 다음, self-play와 강화 학습을 거쳐 Network를 형성할 수 있다.
'CS > 인공지능' 카테고리의 다른 글
| [인공지능] Space Search (1) | 2024.12.11 |
|---|---|
| [인공지능] CNN(Convolutional Neural Network) (0) | 2024.11.30 |
| [인공지능] 딥러닝과 텐서플로 (1) | 2024.11.30 |
| [인공지능] 필기 숫자 데이터 인식 성능 비교 (0) | 2024.11.30 |
| [인공지능] 신경망 (2) | 2024.10.28 |
