Search에 대해 알아보기 전에 다양한 search 방법과 이론들에 대해 알아보자.
Search 이론
상태 공간 트리
상태 공간이란 발생할 수 있는 모든 상태를 포함하는 집합이다. 예를 들어 8-퍼즐의 경우 9! = 362880 크기의 상태 공간을 가진다. 이러한 상태를 연결된 트리 형태로 그리면 상태 공간 트리가 된다.
맹목 탐색
효율적인 전략 없이 정해놓은 순서에 따라서 탐색하는 알고리즘으로 BFS, DFS가 대표적이다. BFS는 최적 해를 보장할까? 그렇다. 왜냐하면 모든 깊이에서 가능한 모든 자식 노드를 살피기 때문이다. 그렇다면, 최적 해를 항상 보장하면서 이동 횟수를 줄일 수는 있을까? 없다. 왜냐하면 모든 노드를 탐색하며 최적 해를 찾는 방법이기 때문이다. 이러한 이유로 BFS는 너무 느리다는 단점이 있다. 그래서 전략적으로 해를 찾는 똑똑한 알고리즘이 필요하다.
최고 우선 탐색
맹목 탐색의 비효율성을 개선하기 위해서 문제의 특성을 반영한 알고리즘이다. 노드의 자식을 평가한 후에 가장 좋은 자식을 먼저 방문하는 방식이다. 예를 들어서, 제자리에 없는 수(불일치 수)를 셀 때 평가 함수로 휴리스틱 함수를 사용할 수 있다. 혹은 제자리를 찾아가는 데 필요한 거리의 합(맨해튼 거리의 합)을 구하는데도 휴리스틱 함수를 사용할 수 있다. 이는 빠르게 처리하기 위해서 우선 순위 큐를 필요로 한다.
A* 알고리즘
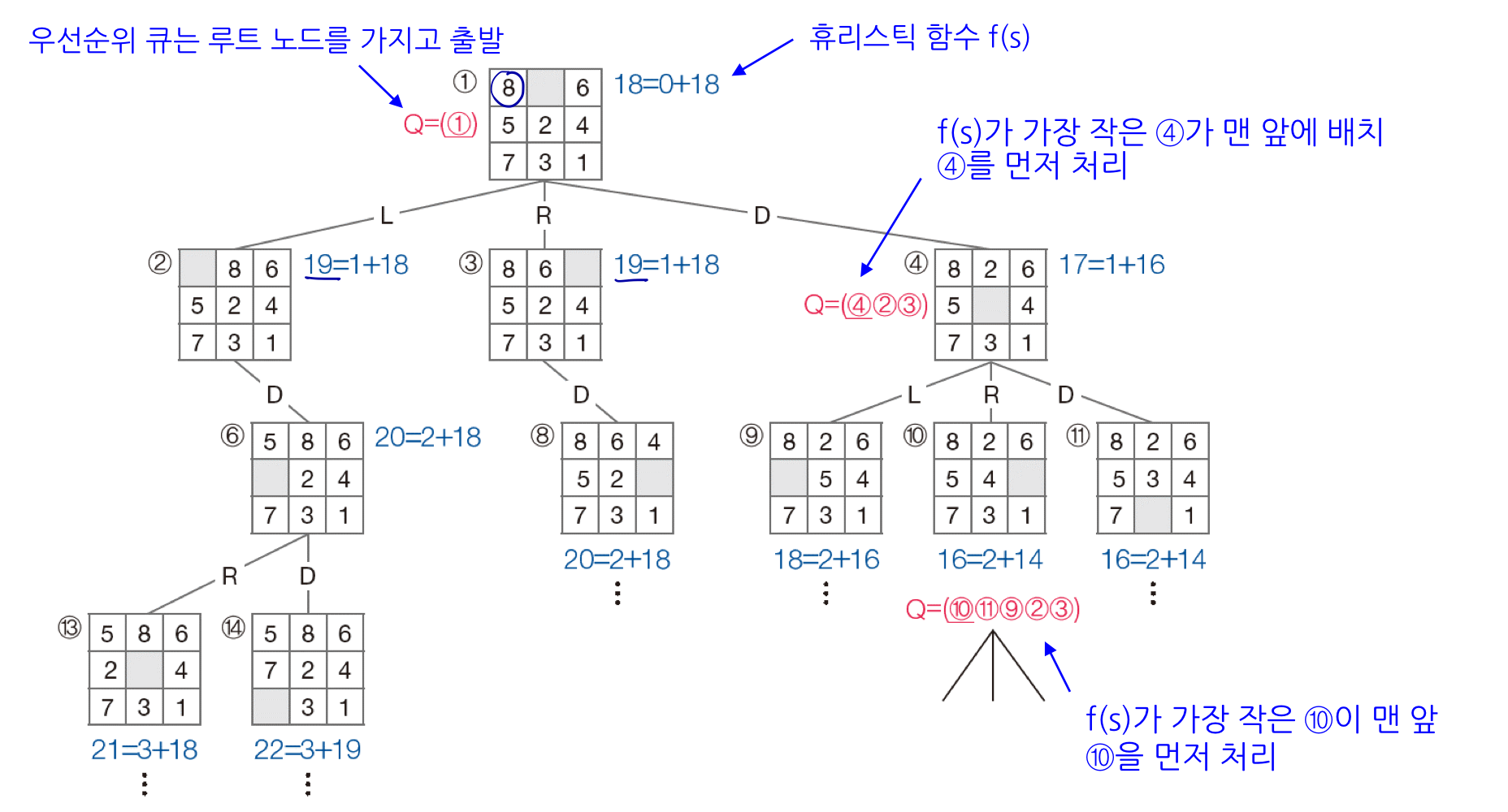
앞선 최고 우선 탐색은 트리를 타고 내려온 이전 기록을 무시한 채로 현재 상황에서 어떤 경로로 트리를 타고 내려가야 할지 결정한다는 한계가 존재한다. 그래서 A* 알고리즘은 이전 기록을 같이 확인한다. f(s) = g(s) + h(s)로 표현할 수 있는데, g(s)는 현재 상태 s까지 찾아오는데 사용한 비용, h(s)는 s에서 목표 상태를 찾아가는데 필요한 비용의 추정치를 말한다.
아래 그림처럼 각 노드의 값을 f(s)를 계산하고 우선순위 큐에 넣어 탐색할 노드를 판단한다. 즉, 현재 보고 있는 노드보다 다른 노드의 f(s)가 더 작은 경우 해당 노드로 이동해서 먼저 탐색한다. 이동 횟수를 줄이는데 최적이다.
미니맥스 알고리즘
지금까지는 혼자 푸는 게임으로 적대적인 상황이 없었다. 이제부터는 체스나 바둑처럼 두 사람이 번갈아 수를 두고 승패를 겨루는 게임으로 확장한다.
틱택토 게임
틱택도 게임은 수평, 수직, 대각 방향으로 세 칸을 먼저 차지한 사람이 이기는 게임이다. 만약에 상대가 어떤 수를 둘 지 모르는데 어떻게 최적의 선택을 할까? 미니맥스 알고리즘에서는 상대도 최적의 수를 둔다고 가정하고 선택한다. 그래서 내가 둘 차례에는 max, 상대방이 둘 차례에는 min을 적용하고 내가 이기면 1, 상대가 이기면 -1, 비기면 0으로 처리한다.
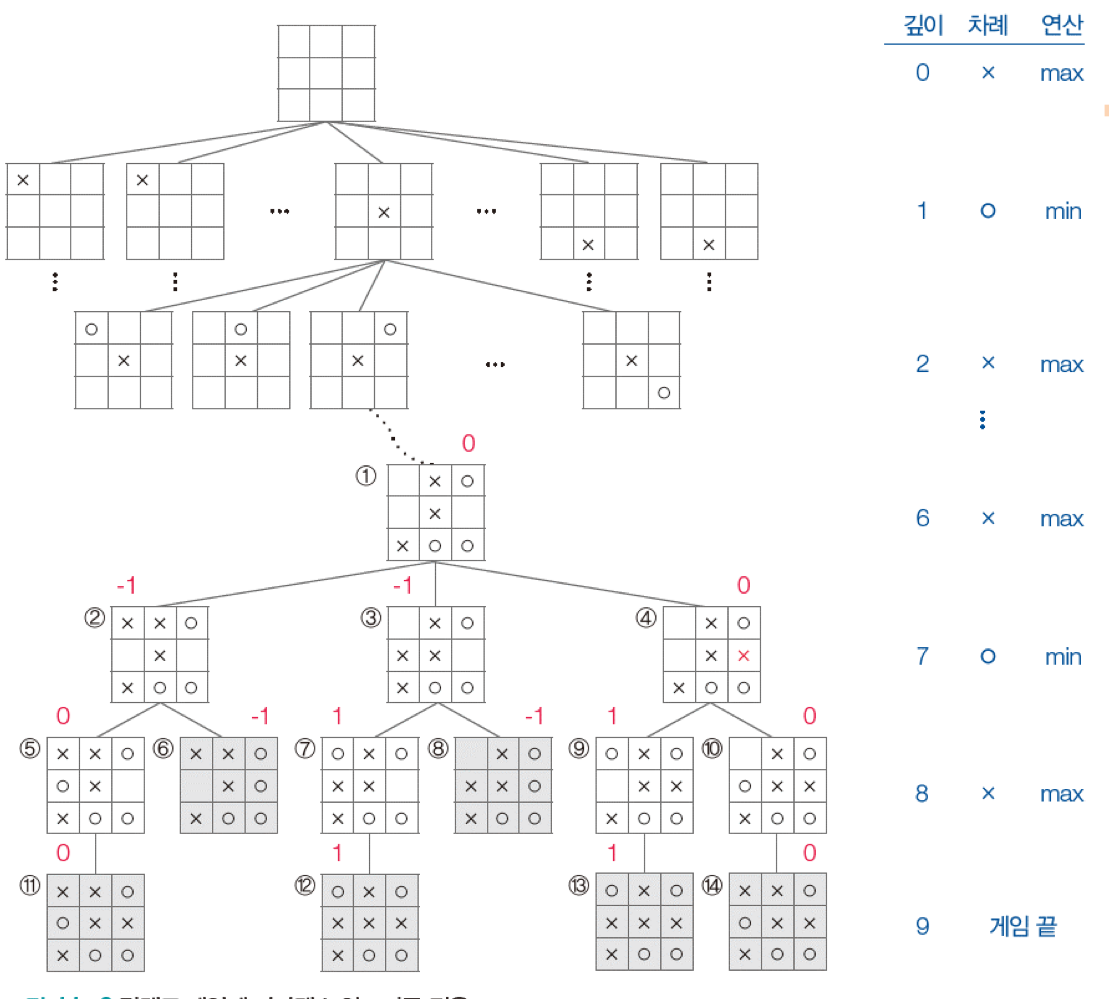
그러나, 미니맥스 알고리즘은 너비 우선 탐색을 하기 때문에 비효율적이다. 바닥 깊이인 9까지 내려가면 8!=40320개의 노드를 모두 탐색해야 한다. 그래서 두 가지 방법을 적용해 비효율성 문제를 해결한다.
먼저, 감당할 수 있는 정도까지만 내려가서 승패가 결정되지 않은 상태에서 휴리스틱 함수를 적용한다.
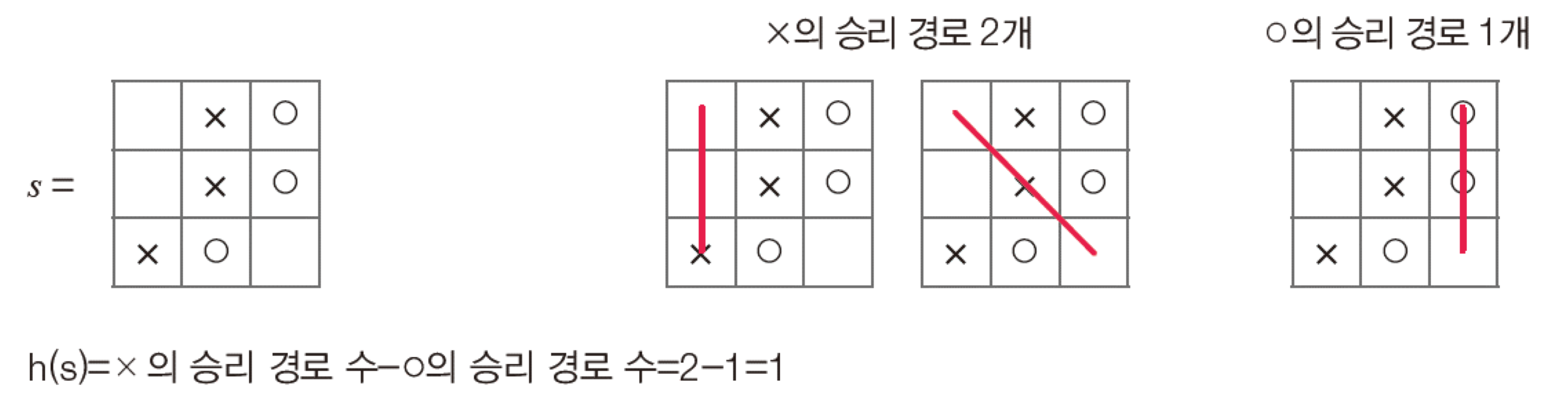
두번째는 알파베타 가지치기 방법이다. 깊이 우선 탐색을 수행하면서 max 혹은 min에서 가지치기를 한다. 아래 그림을 참고해보면, 네모가 자식 노드의 max 값, 동그라미가 자식 노드의 min 값을 취한다고 하자. 2번에서 보면 자식 노드의 min 값을 취해야 하기 때문에 둘 중 작은 값을 선택한다. 이때, 3번은 자식 노드의 max 값을 취하기 때문에 a는 무조건 7보다 작다. 이때, 1번에서 6이 7보다 더 작기 때문에 a를 보지 않아도 2번 값이 결정된다. 그래서 이때 가지치기를 수행한다. 오른쪽 자식노드로 넘어가서, 6번은 min 값을 취한다. 5번까지 계산이 완료된 상태에서 b가 5번 노드 값보다 크게 되면 선택하지 않고, b가 5번 노드보다 작게 되면 선택하지만 4번에서 max 값을 취하기 때문에 선택하지 않는다. 그래서 가치지기를 수행한다.
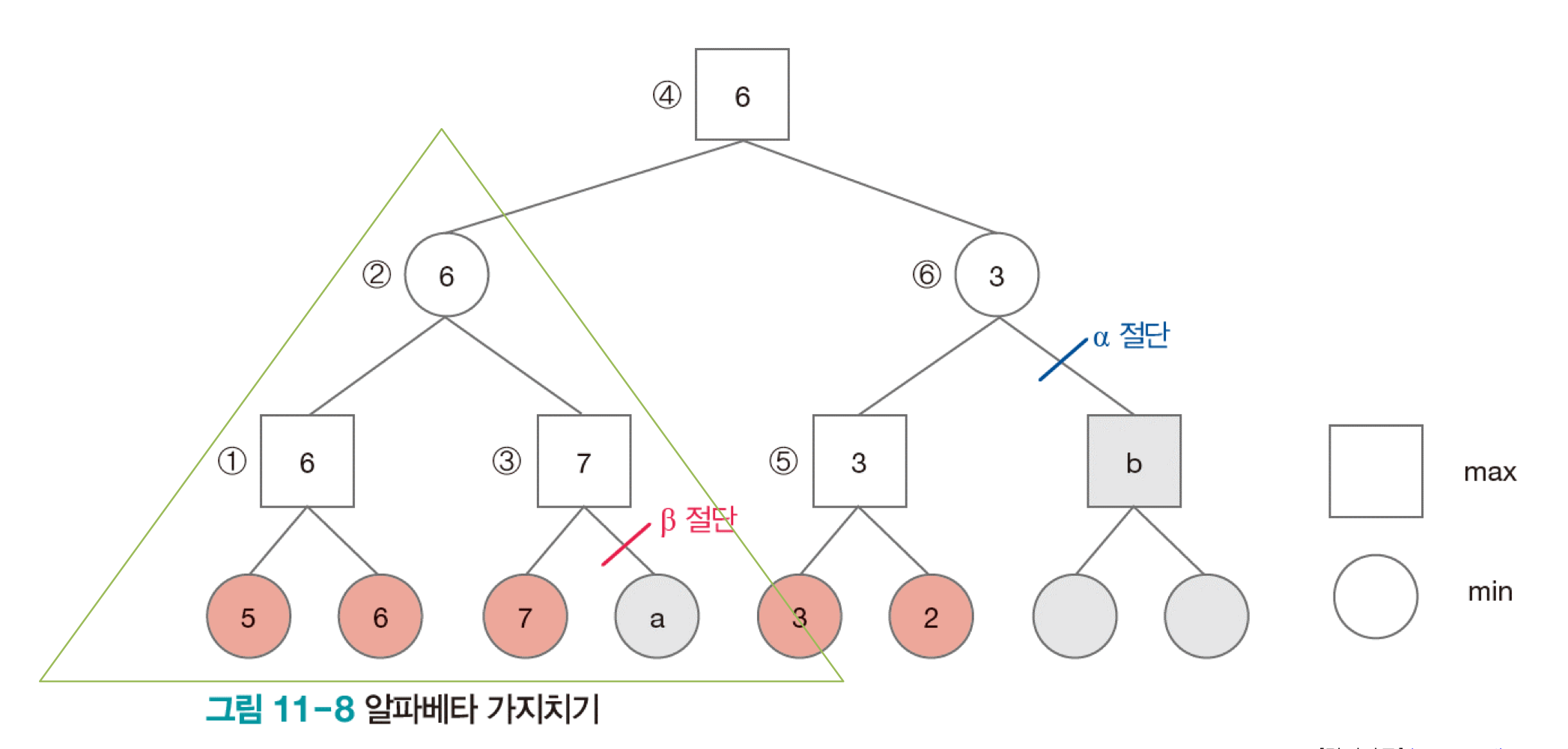
몬테카를로 트리 탐색 알고리즘
미니맥스 알고리즘은 효율적이지만 계산을 과다하게 해야 한다는 것이 한계다. 알파베타 가지치기가 10% 정도 줄여준다고 해도 오랜 시간이 소요된다. 이러한 휴리스틱 함수 없이 탐색 알고리즘을 만들 수 있을까? 몬테카를로 방법은 난수를 생성해 시뮬레이션 하는 기법이다. 횟수를 늘릴수록 통계적 추론이 가능해진다. 이 방법을 활용한 탐색 방법을 Monte Carlo Tree Search, 줄여서 MCTS라고 한다.
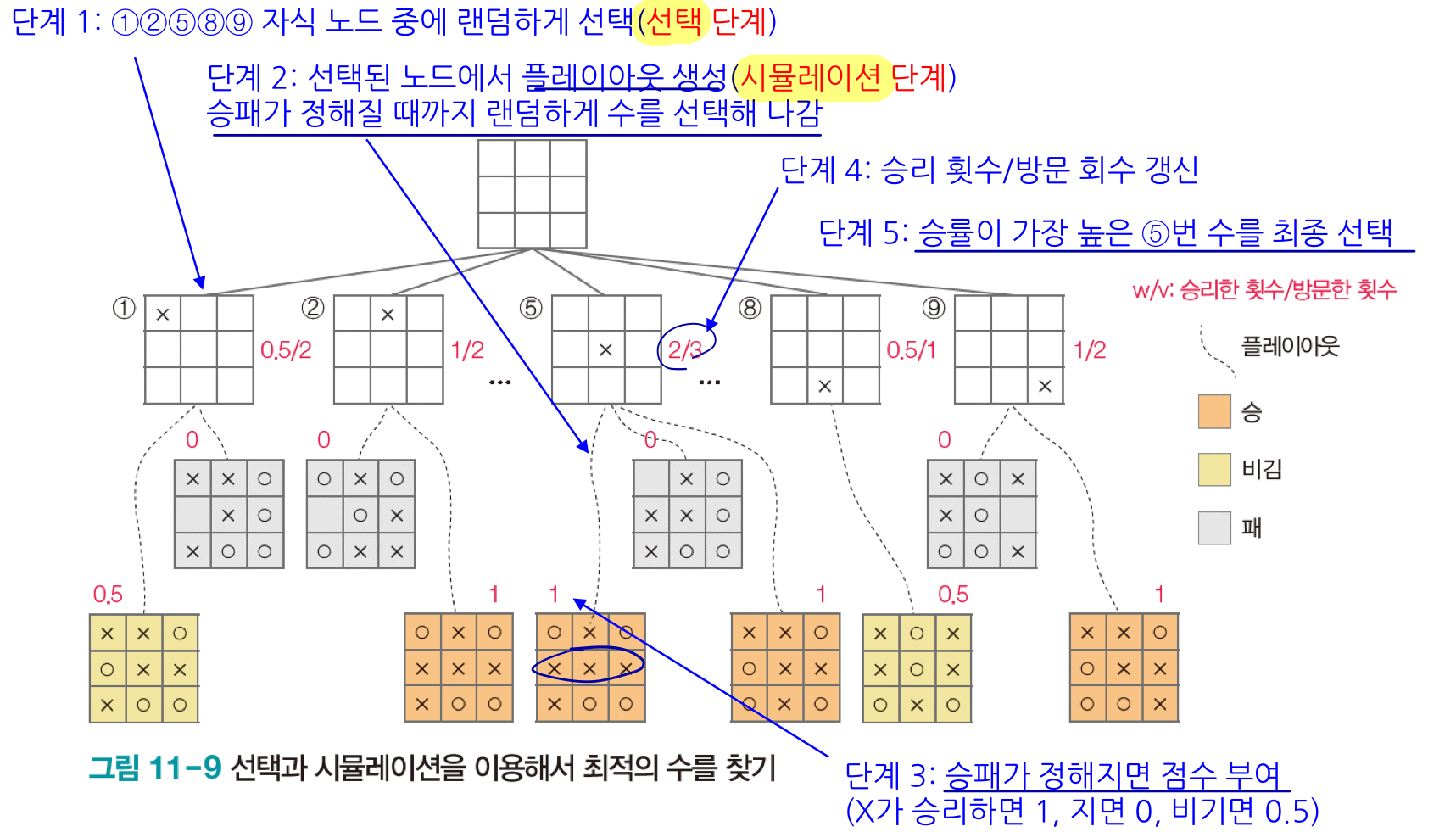
몬테카를로 트리 탐색은 무작위로 수를 선택해 playout을 만들고 승률이 높으면 좋은 수일 가능성이 높다는 것을 바탕으로 한다. 미니맥스는 정교한 휴리스틱 함수를 통해 최적에 가까운 수를 찾는 전략이라면, MCTS는 랜덤하게 수를 두고 승률이 높은 수를 최적에 가까운 수로 간주한다. 따라서 휴리스틱 함수를 설계할 필요가 없고 게임 종료 상태까지 보기 때문에 계산이 쉽다는 장점이 있다. 결국 샘플이 많을수록 확률적 접근이 가능해져 정확도가 높아진다. 이러한 것이 기본적인 원리인데, 성능을 조금 더 개선할 수 있다.
먼저, 몬테가를로 트리 탐색의 처리 절차를 살펴보자. 인공지능은 자신의 차례가 되면 현재 상태를 root로 설정하고 네 단계를 적용해 최적의 수를 결정하고 두면 된다.
- 선택 : 루트에서 시뮬레이션 되지 않은 노드를 선택해서 leaf node에 닿을 때까지 내려간다. 좋은 것을 자주 선택하지만 아직 시도하지 않은 것도 균형잡힌 전략이 필요하기 때문에 UCT(upper confidence tree) 전략을 사용한다.
- 확장 : 단말 노드의 자식 중에 랜덤하게 하나를 선택한다.
- 시뮬레이션 : 노드 c에서 시작해서 게임이 종료될 때까지 진행해 플레이아웃을 하나 만들고 누가 승리했는지 판정한다.
- 역전파 : c에서 시작해서 트리를 역으로 올라가면서 root까지 경로에 있는 노드의 v와 w를 갱신한다.
'CS > 인공지능' 카테고리의 다른 글
| [인공지능] Reinforcement Learning (3) | 2024.12.11 |
|---|---|
| [인공지능] CNN(Convolutional Neural Network) (0) | 2024.11.30 |
| [인공지능] 딥러닝과 텐서플로 (1) | 2024.11.30 |
| [인공지능] 필기 숫자 데이터 인식 성능 비교 (0) | 2024.11.30 |
| [인공지능] 신경망 (2) | 2024.10.28 |
